Blabla 15-18 ans

n°29

Avec cette photo ça sera beaucoup mieux

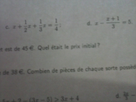
si quelqu'un pouvait me faire ces deux petites équations. J'ai un contrôle demain et je comprend pas car j'ai été absent. Merci;

mr-ehf C'est strictement supérieur ou alors supérieur ou égal?

Mondial
x + x/2 + x/3 = 1/4
6x/6 + 3x/6 + 2x/6 = 1/4
11x/6 = 1/4
x = 6/44 = 3/22

x + (x-1)/3 = 5
4x/3 = 15/3 + 1/3 = 16/3
x = 4

Merci encore, Dowie.

Strictement supérieur où egal

please je comprend rien

mr-ehf
C'est pas possible alors : une fonction constante est à la fois croissante et décroissante.
Si on a pour tout x réel f(x) = g(x) = f(1), pour x>1 on a tout de même f(x) = g(x)

Erreur d'énoncé

Arrange toi pour le mettre droit et je te le fais linkds

Supérieur strictement je pense

ah désolé voila

Partie A)
1)
Il y a trois boules rouges et n boules au total donc il y a n-3 boules blanches.
La probabilité de tirer une boule blanche est donc
pn = (n-3)/n

2)
On a rajouté une boule blanche. Il y a donc maintenant n-2 boules blanches et n+1 boules au total.
qn = (n-2)/(n+1)

Partie B:
Soit x appartenant à [3;+oo[
f(x) = (x-3)/x = 1 - 3/x
f est la composée de la fonction inverse par la fonction affine x->1-3x. Cette fonction affine a un coefficient directeur strictement négatif, elle est donc strictement décroissante sur R

La fonction inverse est strictement décroissante sur ]3;+oo[.
f est la composée de deux fonctions strictement décroissante, elle est donc croissante.

g(x) = (x-2)/(x+1) = (x+1 - 3)/(x+1) = 1 - 3/(x+1)
g est la composée de x->x+1 par f. x->x+1 est une fonction affine au coefficient directeur strictement positive, elle est donc strictement croissante.
g est la composée de deux fonctions strictement croissante, elle est donc strictement croissante.

2 à 4) c'est du graphique

5) Ce résultat était prévisible. En effet, dans le deuxième cas de figure, on rajoute une boule blanche. On augmente donc la proportion de boule blanche dans l'urne ce qui augmente la probabilité de tirer une boule blanche

merci !!!!! mec je t'aime (façon de parler hein )

Salut Dowie !
Peux tu m'aider pour la question 2)b de l'exercice 2 :

Salut

Tu t'y connais en dérivée d'exponentielle ?

Si oui, quel est la dérivée de 2e^x (e^x-1) ? (^x = puissance x, si jamais )

Tu peux aussi m'aider sur le 1 de l'exercice 3 stp ?

ma calculatrice déconne

Trace la courbe en calculant des points non ? genre f(0); f(1); f(2); f(-1); f(-2) ...ça devrait t'aider

même google peut te la tracer