Savoir & Culture

Ola les amis matheux

Petit dilemme, j'ai besoin de savoir comment calculer la valeur d'un segment/longueur par rapport à 2 figures (cercle/triangle):

Comment connaitre la valeur de "C" ?
Par exemple:

- rayon "r" = 10

Merci les gens !!!

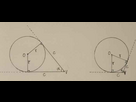
Tu connais l'angle beta entre tes deux rayons car tu sais que la somme des angles d'un quadrilatère c'est 2pi et tu connais les 3 autres angles. Beta = pi-alpha

Tu peux donc calculer la longueur L de la corde du cercle (qui relie les deux points où tu as mis des angles droits) avec la loi les cosinus : L^2 = 2r^2(1-cos(beta)).

En utilisant la loi des cosinus une nouvelle fois tu peux aussi exprimer L^2 en fonction de C et alpha : L^2 = 2C^2(1-cos(alpha)).

Tu peux ensuite isoler facilement le C en utilisant les deux expressions de L^2.

ya le VI de GTA VI dans le cercle en fesant pro alpha - C au carré fois Pi

Oula vous m'avez perdu là.... Je cale que dalles :D

Possible de me faire la formule en utilisant les lettres du dessin ? Merci ;)

r/tan(alpha/2)

Le 02 novembre 2023 à 10:17:31 :
Tu connais l'angle beta entre tes deux rayons car tu sais que la somme des angles d'un quadrilatère c'est 2pi et tu connais les 3 autres angles. Beta = pi-alpha

Tu peux donc calculer la longueur L de la corde du cercle (qui relie les deux points où tu as mis des angles droits) avec la loi les cosinus : L^2 = 2r^2(1-cos(beta)).

En utilisant la loi des cosinus une nouvelle fois tu peux aussi exprimer L^2 en fonction de C et alpha : L^2 = 2C^2(1-cos(alpha)).

Tu peux ensuite isoler facilement le C en utilisant les deux expressions de L^2.

C est pas genre 10 fois trop compliqué ?

Le 02 novembre 2023 à 10:17:31 :
Tu connais l'angle beta entre tes deux rayons car tu sais que la somme des angles d'un quadrilatère c'est 2pi et tu connais les 3 autres angles. Beta = pi-alpha

Tu peux donc calculer la longueur L de la corde du cercle (qui relie les deux points où tu as mis des angles droits) avec la loi les cosinus : L^2 = 2r^2(1-cos(beta)).

En utilisant la loi des cosinus une nouvelle fois tu peux aussi exprimer L^2 en fonction de C et alpha : L^2 = 2C^2(1-cos(alpha)).

Tu peux ensuite isoler facilement le C en utilisant les deux expressions de L^2.

je sais même pas si c'est un troll