Blabla 15-18 ans

Et pour les formule : 0.5(nV^2 + nU^2 -(nV-nU)^2) et 0.5((nV + Vu)^2 - nV^2 - nU^2).

Est-ce que c'est la même chose ? Est-ce que l'une est a privilégier selon si la forme étudiée est un parrallélogramme ou un triangle ?

PS : n = || = norme.

Et pour les formule : 0.5(nV^2 + nU^2 -(nV-nU)^2) et 0.5((nV + Vu)^2 - nV^2 - >nU^2).

Attention, ||u + v|| ce n'est pas forcément égal à ||u|| + ||v||
Donc, la formule du produit scalaire des vecteurs u et v c'est plutôt :
(1) : (1/2)*(||u||^2 + ||v||^2 - ||u - v||^2)
ou
(2) : (1/2)*(||u + v||^2 - ||u||^2 - ||v||^2)

Est-ce que c'est la même chose ?

Oui

Est-ce que l'une est a privilégier selon si la forme étudiée est un parrallélogramme ou un triangle ?

Sachant le vecteur AB est égal au vecteur -BA, il faut choisir la formule qui te permet d'utiliser la relation de Chasles

Par exemple si on a un parallélogramme ABCD et qu'on, on connaît toutes ses longueurs.
Pour le produit scalaire AB.BC il faut utiliser la formule (2) car
||AB + BC||^2 = ||AC||^2
Pour le produit scalaire CA.CD il faut utiliser la formule (1) car
||CA - CD||^2 = ||CA + DC||^2 = ||DA||^2

Le 19 décembre 2023 à 19:32:26 :
Salut tu peux me faire mon dm de spé math

Dans la partie C de l'exercice 2, il y a un alpha à partir de la question 2.b) mais il n'est définit nul part. Soit tu ne m'as pas tout envoyé, soit ton prof a oublié de mettre des infos dans l'énoncé et je pense qu'elles sont essentielles pour répondre aux questions.

Je suppose qu'alpha c'est un réel dans J qui vérifie f(alpha) = alpha

Le 20 décembre 2023 à 22:49:32 :

Le 19 décembre 2023 à 19:32:26 :
Salut tu peux me faire mon dm de spé math

Dans la partie C de l'exercice 2, il y a un alpha à partir de la question 2.b) mais il n'est définit nul part. Soit tu ne m'as pas tout envoyé, soit ton prof a oublié de mettre des infos dans l'énoncé et je pense qu'elles sont essentielles pour répondre aux questions.

Je suppose qu'alpha c'est un réel dans J qui vérifie f(alpha) = alpha

J'ai l'impression qu'il manque des questions dans la partie B de cet exercice car on s'intéresse à l'intersection de (C) et (Delta) mais on ne conclut jamais sur l'existence de cette intersection et son encadrement. Et la partie C m'indique fortement que J est l'intervalle dans lequel ce trouve cet alpha.

Le 19 décembre 2023 à 19:32:26 :
Salut tu peux me faire mon dm de spé math

Et il n’y a plus de questions après la 3-a) de la partie D de l’exo 2

Le 21 décembre 2023 à 13:10:13 :
Et concernant la question 2b il ma dit que il n’y achn problème et qu’il fallait s aider de la question précédente la 2b jcrois c une limite et c normal que alpha nous est pas donné

Ils doivent au moins dire "avec alpha un réel"

Le 21 décembre 2023 à 13:09:25 :
Oui après la question 3)a le dm est fini

Ça n'a pas de sens, pourquoi c'est la question 3.a) et pas la question 3. tout simplement ? Après ton prof s'est peut-être juste trompé.

Le 21 décembre 2023 à 13:10:13 :
Et concernant la question 2b il ma dit que il n’y achn problème et qu’il fallait s aider de la question précédente la 2b jcrois c une limite et c normal que alpha nous est pas donné

Le problème c'est que alpha n'est définit nul part et normalement il doit être introduit quelque part dans l'énoncé car je ne suis pas sûr que cette inégalité soit vraie pour n'importe quelle valeur de alpha.

Je vais t'envoyer ce que j'ai fait, mais si tu as d'autres infos ou si c'est moi qui me suis trompé j'essayerai de rectifier.

Le 21 décembre 2023 à 13:38:09 :

Le 21 décembre 2023 à 13:09:25 :
Oui après la question 3)a le dm est fini

Ça n'a pas de sens, pourquoi c'est la question 3.a) et pas la question 3. tout simplement ? Après ton prof s'est peut-être juste trompé.

Le 21 décembre 2023 à 13:10:13 :
Et concernant la question 2b il ma dit que il n’y achn problème et qu’il fallait s aider de la question précédente la 2b jcrois c une limite et c normal que alpha nous est pas donné

Le problème c'est que alpha n'est définit nul part et normalement il doit être introduit quelque part dans l'énoncé car je ne suis pas sûr que cette inégalité soit vraie pour n'importe quelle valeur de alpha.

Je vais t'envoyer ce que j'ai fait, mais si tu as d'autres infos ou si c'est moi qui me suis trompé j'essayerai de rectifier.

D'ailleurs, alpha est nécessairement dans J, car sinon on n'aurait pas la majoration du 3eme point de la question 3.a), ou en tout cas il ne peut pas être en dehors de l'intervalle [0,2 ; 0,4]

Le 19 décembre 2023 à 19:32:26 :
Salut tu peux me faire mon dm de spé math

Exercice 1

Dans l’énoncé il y a écrit Pn = p(An) mais je suppose que c’est plutôt pn = P(An)

Notation : P(A I B) = PB(A) = « Probabilité de l’événement A sachant que l’événement B est réalisé »

Arbre à 2 niveaux

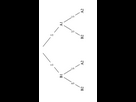
1.
p1 = P(A1) = 1/2

D’après la formule des probabilités totales on a
p2 = P(A2) = P(A2 I A1)*P(A1) + P(A2 I B1)*P(B1)
P(A2 I A1) = 1/3
P(A2 I B1) = 1/5
P(A1) = p1 = 1/2
P(B1) = p1 = 1/2
p2 = (1/3)*(1/2) + (1/5)*(1/2) = 1/6 + 1/10 = 5/30 + 3/30 = 8/30 = 4/15

2.
Démonstration par récurrence
Hn : pn = (2/15)*pn-1 + 1/5

- Initialisation : n = 2
p2 = 4/15
(2/15)*p1 + 1/5 = (2/15)*(1/2) + 1/5 = 2/30 + 1/5 = 2/30 + 6/30 = 8/30 = 4/15 = p2
Hn est vraie au premier rang

- Hérédité :
Supposons qu’il existe un entier naturel n supérieur ou égal à 2 tel que Hn soit vraie
Montrons que Hn+1 est vraie, c’est à dire pn+1 = (2/15)*pn + 1/5
D’après la formule de probabilités totales on a
pn+1 = p(An+1) = P(An+1 I An)*P(An) + P(An+1 I Bn)*P(Bn)
P(An+1 I An) = 1/3
P(An+1 I Bn) = 1/5
P(An) = pn
P(Bn) = 1 - P(An) = 1 - pn
pn+1 = (1/3)*pn + (1/5)*(1 - pn) = (1/3)*pn + 1/5 - (1/5)*pn = (5/15)*pn - (3/15)*pn + 1/5 = (2/15)*pn + 1/5
Hn+1 est vraie

- Conclusion :
Par récurrence, pour tout entier naturel n supérieur ou égal à 2 Hn est vraie

3.
un+1 = pn+1 - 3/13 = (2/15)*pn + 1/5 - 3/13 = (2/15)*pn + 13/65 - 15/65 = (2/15)*pn - 2/65 = (2/15)*(pn - 15/65) = (2/15)*(pn - 3/13) = (2/15)*un
La suite (un) est une suite géométrique de raison q = 2/15
Le premier terme est u1 = p1 - 3/13 = 1/2 - 3/13 = 13/26 - 6/26 = 7/26

4.
un = u1*q^n = (7/26)*(2/15)^n
pn = un + 3/13 = (7/26)*(2/15)^n + 3/13

5.
0 < 2/15 < 1
=> lim +inf (2/15)^n = 0
=> lim +inf pn = (7/26)*0 + 3/13 = 3/13

Exercice 2

Partie A

1.
Soit u(x) = x^2 - 2x + 2, un polynôme de degré 2
Calcul du discriminant
Delta = (-2)^2 - 4*1*2 = 4 - 8 = -4 < 0
Le signe de ce polynôme pour tout x réel est celui de son coefficient dominant qui est 1 > 0
Donc pour tout réel x, x^2 - 2x + 2 > 0

2.
f(x) = ln(u(x))
f’(x) = u’(x)/u(x)
u’(x) = 2x - 2 = 2*(x - 1)
f’(x) = 2*(x - 1)/(x^2 - 2x + 2)

On a vu dans la question 1. que pour tout réel x, x^2 - 2x + 2 > 0 donc le signe de f’ est le même que celui de x - 1, qui est négatif sur ]-inf ; 1] et positif sur [1 ; + inf[
Donc f est décroissante sur ]-inf ; 1] et croissante sur [1 ; + inf[

3.
Le coefficient dominant du polynôme u est positif
=> lim +inf u(x) = lim -inf u(x) = +inf
=> lim +inf f(x) = lim -inf f(x) = +inf

4.
Représentation de (C) et (Delta)

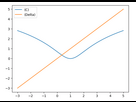
u(1 + x) = (1 + x)^2 - 2*(1 + x) + 2 = 1 + 2x + x^2 - 2 - 2x + 2 = x^2 + 1
u(1 - x) = (1 - x)^2 - 2*(1 - x) + 2 = 1 - 2x + x^2 - 2 + 2x + 2 = x^2 + 1
u(1 + x) = u(1 - x) donc la droite d’équation x = 1 est un axe de symétrie de (C)

Représentation de la symétrie

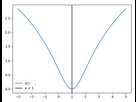
f(0) = ln(2)
f’(0) = 2*(-1)/2 = -1 < 0
T0(1) = f’(0)*1 + f(0) = -1 + ln(2)
La tangente au point d’abscisse 0, T0 passe par les points (0, ln(2)) et (1, -1 + ln(2))
Par symétrie par rapport à l’axe x = 1, la tangente au point d’abscisse 2 T2, passe par les points (2, ln(2)) et (1, -1 + ln(2))

Représentation des tangentes

Représentation globale

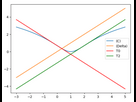
Partie B

1.
phi’(x) = f’(x) - 1 = 2*(x - 1)/(x^2 - 2x + 2) - 1
phi’’(x) = f’’(x)
Soit v1(x) = (x - 1) et v2(x) = x^2 - 2x + 2
v1’(x) = 1 et v2’(x) = 2x - 2 = 2*(x - 1)
f’’(x) = 2*(v1’(x)*v2(x) - v1(x)*v2’(x))/(v2(x))^2
v1’(x)*v2(x) = x^2 - 2x + 2
v1(x)*v2’(x) = 2*(x - 1)^2 = 2*(x^2 - 2x + 1) = 2x^2 - 4x + 2
v1’(x)*v2(x) - v1(x)*v2’(x) = x^2 - 2x + 2 - 2x^2 + 4x - 2 = -x^2 + 2x = x*(1 - x)
phi’’(x) = f’’(x) = 2x*(1 - x)/(x^2 - 2x + 2)^2

Pour tout x réel, (x^2 - 2x + 2)^2 > 0
=> le signe de phi’’ est celui de x*(1 - x) = -x^2 - x
Le coefficient dominant de ce polynôme est -1 < 0 et ses racines sont 0 et 1
phi’’ est négative sur ]-inf ; 0[, positive sur [0 ; 1] et négative sur [1 ; +inf[
=> phi’ est décroissante sur ]-inf ; 0[, croissante sur [0 ; 1] et décroissante sur [1 ; +inf[
lim phi’ -inf = 0 - 1 = -1 < 0
=> phi’ est strictement négative sur ]-inf ; 0] donc phi est strictement décroissante sur cet intervalle
sur l’intervalle [0 ; +inf[ phi’ atteint sont maximum en 1
phi’(1) = f’(1) - 1 = 0 - 1 = -1 < 0
phi’ est strictement négative sur [0 ; +inf[ donc phi est strictement décroissante sur cet intervalle

phi est strictement décroissante sur R

2.a)
phi(-x) = f(-x) + x = ln(x^2 + 2x + 2) + x
lim +inf f(-x) = +inf
lim -inf phi(x) = lim +inf phi(-x) = +inf

2.b)
x*(2*ln(x)/x + ln(1 - 2/x + 2/x^2)/x - 1)
= 2*ln(x) + ln(1 - 2/x + 2/x^2) - x
= ln(x^2) + ln(1 - 2/x + 2/x^2) - x
= ln(x^2*(1 - 2/x + 2/x^2)) - x
= ln(x^2 - 2x + 2) - x
= phi(x)

Par croissance comparée, lim +inf 2*ln(x)/x = 0
lim +inf 1 - 2/x + 2/x^2 = 1
=> lim +inf ln(1 - 2/x + 2/x^2) = ln(1) = 0
Alors, lim + inf phi est équivalente à lim +inf x*(0 + 0 - 1) = -x = -inf

Partie C

1.
u(x) = x^2 - 2x + 2
u’(x) = 2x - 2 = 2*(x - 1)
u’ est négative sur ]-inf ; 1] donc x^2 - 2x + 2 est strictement décroissante sur ]-inf ; 1]
Comme J est inclus dans cet intervalle, x^2 - 2x + 2 est décroissante sur J.
=> f est décroissante sur J
f(0,3) = 0,399 à 10^-3 près
f(0,4) = 0,307 à 10^-3 près
Donc si x appartient à J, f(x) appartient à J

2.a)
f’(x) = 2*(x - 1)/(x^2 - 2x + 2)
f’’(x) = 2x*(1 - x)/(x^2 - 2x + 2)^2
f’’ est positive sur J donc f’ est croissante sur J
f’(0,3) = -0,94 à 10^-2 près
f’(0,4) = -0,88 à 10^-2 près
Donc pour tout x de J, abs(f’(x)) <= 0,95

2.b)
Dans la partie C, on a vu que la fonction phi était strictement décroissante sur R.
phi(0,3) = 0,099 à 10^-3 près
phi(0,4) = -0,093 à 10^-3 près
phi étant continue sur R, d’après le théorème des valeurs intermédiaires, il existe un réel alpha dans l’intervalle J tel que phi(alpha) = 0
=> f(alpha) - alpha = 0
=> f(alpha) = alpha

D’après l’inégalité des accroissements finis, pour tout a et b dans J
abs(f(a) - f(b)) <= 0,95*abs(a - b)
Donc pour tout x dans J et avec b = alpha on a
abs(f(a) - alpha) <= 0,95*abs(x - alpha)

Si tu n’as jamais vu cette inégalité, ça se retrouve en passant par le calcul intégrale :
D’après la question 2.a) on a pour tout x dans J
-0,95 <= f’(x) <= 0,95
En intégrant sur un intervalle [a ; b] inclus dans J on a
-0,95*(b - a) <= f(b) - f(a) <= 0,95*(b - a)
si b =/= a
=> -0,95 <= (f(b) - f(a))/(b - a) <= 0,95
=> abs(f(b) - f(a))/(b - a)) <= 0,95
=> abs(f(b) - f(a)) <= 0,95*abs(b - a)
Donc pour tout x dans J et avec a = alpha on a
abs(f(x) - alpha) <= 0,95*abs(x - alpha)

Si tu n’as pas encore vu le calcul intégral, je n’ai pas d’idée pour cette question.

3.a)
Point 1 :
u0 dans J
D’après la question 1.
=> u1 = f(u0) dans J
=> u2 = f(u1) dans J
…
=> un = f(un-1) dans J

Point 2 :
Comme le point 1 est vérifié, ça découle de la question 2.b.

Point 3 :
Démonstration par récurrence
Hn : abs(un - alpha) <= 0,1*0,95^n

- Initialisation : n = 0
abs(u0 - alpha) = abs(0,3 - alpha)
- 0,1 <= 0,3 - alpha <= 0
Alors, abs(u0 - alpha) <= 0,1 = 0,1*0,95^0
Hn est vraie au premier rang

- Hérédité :
Supposons qu’il existe un entier naturel n tel que Hn soit vraie, montrons que Hn+1 est vraie, c’est à dire abs(un+1 - alpha) <= 0,1*0,95^(n+1)
D’après le point 2
abs(un+1 - alpha) <= 0,95*abs(un - alpha) <= 0,95*0,1*0,95^n = 0,1*0,95^(n+1)
Hn+1 est vraie

- Conclusion :
Par récurrence, pour tout entier naturel n, Hn est vraie

Soit l = limite +inf un
0 < 0,95 < 1 => lim +inf 0,95^n = 0
Donc d’après le point 3
abs(l - alpha) <= 0,1*0 = 0
La suite (un) converge vers alpha

3.b)
On utilise le point 3
0,1*0,95^n = 10^(-3)
=> 0,95^n = 10^(-2)
=> ln(0,95^n) = ln(10^(-2)) = -2*ln(10)
=> n*ln(0,95) = -ln(100)
=> n = -ln(100)/ln(0,95)
=> n = 89,8 à 10^-1 près

En arrondissant à l’entier supérieur on a n0 = 90

Partie D

1.
(1/4)^2 - 2*(1/4) + 2
= 1/16 - 1/2 + 2
1/16 - 8/16 + 32/16
25/16

f(1/4) = ln(25/16)

1/4 - 1 = 1/4 - 4/4 = -3/4

f’(1/4) = 2*(-3/4)/(25/16) = (-2*3*16)/(4*25) = -24/25

La tangente (T) à la courbe C au point d’abscisse 1/4 a pour équation
y = f’(1/4)*(x - 1/4) + f(1/4) = -(24/25)*(x - 1/4) + ln(25/16) = -(24/25)*x + 24/(4*25) + ln(25/16) = -(24/25)*x + 6/25 + ln(25/16)

2.
La droite (EF) a pour équation y = ax + b
f(0) = ln(2), la droite (EF) passe par le point E de coordonnées (0, ln(2))
(1/2)^2 - 2*(1/2) + 2 = 1/4 + 1 + 2 = 1/4 + 1 = 1/4 + 4/4 = 5/4
f(1/2) = ln(5/4), la droite (EF) passe par le point F de coordonnées (1/2, ln(5/4))
a = (f(1/2) - f(0))/(1/2 - 0) = 2*(f(1/2) - f(0))
f(1/2) - f(0) = ln(5/4) - ln(2) = ln(5/(4*2)) = ln(5/8)
a = 2*ln(5/8)
(EF) passe par E
ln(2) = 2*ln(5/8)*0 + b = b

y = 2*ln(5/8) + ln(2)

3.a)
ln(5/4) = 0,22 à 10^-2 près
(1/4)*ln(5/2) = 0,23 à 10^-2 près
Donc A = 0,225 à 5*10^-3 près

Le 25 décembre 2023 à 13:56:53 :

1.a.
f(1) = 1^2 + 6*1 - 7 = 1 + 6 - 7 = 7 - 7 = 0
1 est racine de f, donc il existe des réels a et b tels que f(x) = (x - 1)*(ax + b)
f(x) = (x - 1)*(ax + b) = ax^2 - ax + bx - b = a*x^2 + (b - a)*x + (-b) = 1*x^2 + 6*x + (-7)
par identification on a
a = 1
b - a = 6
b = 7
=>
a = 1
b = 7
La forme factorisée de f est f(x) = (x - 1)*(x + 7)

On en déduite la deuxième racine du polynôme f :
x + 7 = 0 <=> x = -7

Le coefficient dominant de f est 1 qui est positif

f est négative entre ses racines, c’est à dire sur l’intervalle [-7 ; 1] et positive ailleurs, c’est à dire sur l’intervalle ]-inf ; -7] et l’intervalle [1 ; +inf[

Tableau de signe de f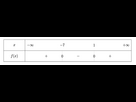

1.b.
On développe l’expression factorisée pour retrouver g
(-2x + 7)*(2x + 3) = -4x^2 + 14x - 6x + 21 = -4x^2 + 8x + 21 = g(x)

On utilise la forme factorisée de g pour trouver ses racines :
-2x + 7 = 0 <=> -2x = -7 <=> x = 7/2
2x + 3 = 0 <=> 2x = -3 <=> x = -3/2

Le coefficient dominant de g est -4 qui est négatif

g est positive entre ses racines, c’est à dire sur l’intervalle [-3/2 ; 7/2] et négative ailleurs, c’est à dire sur l’intervalle ]-inf ; -3/2] et l’intervalle [7/2 ; +inf[

Tableau de signe de g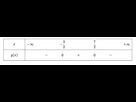

1.c.
h(x) = 9x^2 - 6x + 1 = (3x)^2 - 2*3x*1 + 1^2 (on reconnaît une identité remarquable)
h(x) = (3x - 1)^2
Pour tout réel x, h(x) est positive.
Elle s’annule au point vérifiant 3x - 1 = 0 <=> 3x = 1 <=> x = 1/3

1.d.
On développe l’expression pour retrouver i(x)
3*(x + 2)^2 + 8 = 3*(x^2 + 2*2x + 2^2) + 8 = 3*(x^2 + 4x + 4) = 3x^2 + 12x + 12 + 8 = 3x^2 + 6x + 20 = i(x)
Pour tout réel x, (x + 2)^2 est positive
Donc pour tout réel x, i(x) est strictement positive et donc ne s’annule jamais.

2.
Courbe représentative de f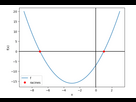

Les branches de la parabole sont tournées vers le haut, donc f est négative entre ses racines et positive ailleurs.

Courbe représentative de g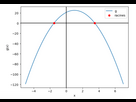

Les branches de la parabole sont tournées vers le bas, donc g est positive entre ses racines et négative ailleurs.

Courbe représentative de h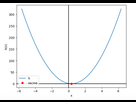

Les branches de la parabole sont tournées vers le haut, la parabole coupe l’axe des abscisses en 1 point, donc h est positive partout.

Courbe représentative de i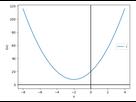

Les branches de la parabole sont tournées vers le haut, la parabole ne coupe pas l’axe des abscisses, donc i est strictement positive partout.

3.a.
Courbe 1 :
- Les branches de la parabole sont tournées vers le haut, donc le signe de a est positive
- La courbe est décroissante sur ]-inf ; -b/2a] et croissante sur [-b/2a ; +inf[ donc le discriminant est négatif sur ]-inf ; -b/2a] et positif sur [-b/2a ; +inf[
- f possède deux racines, x1 < x2, donc f est négative entre ses racines et positive ailleurs
Tableau de signe de f

Courbe 2 :
- Les branches de la parabole sont tournées vers le bas, donc le signe de a est négatif
- La courbe est croissante sur ]-inf ; -b/2a] et décroissante sur [-b/2a ; +inf[ donc le discriminant est positif sur ]-inf ; -b/2a] et négatif sur [-b/2a ; +inf[
- f possède 2 racines, x1 < x2, donc f est positive entre ses racines et négative ailleurs
Tableau de signe de f

Courbe 3 :
- Les branches de la parabole sont tournées vers le bas, donc le signe de a est négatif
- La courbe est croissante sur ]-inf ; -b/2a] et décroissante sur [-b/2a ; +inf[ donc le discriminant est positif sur ]-inf ; -b/2a] et négatif sur [-b/2a ; +inf[
- f possède 1 racine, x0, donc f est négative partout
Tableau de signe de f

Courbe 4 :
- Les branches de la parabole sont tournées vers le haut, donc le signe de a est positif
- La courbe est décroissante sur ]-inf ; -b/2a] et croissante sur [-b/2a ; +inf[ donc le discriminant est négatif sur ]-inf ; -b/2a] et positif sur [-b/2a ; +inf[
- f possède 1 racine, x0, donc f est positive partout
Tableau de signe de f

Courbe 5 :
- Les branches de la parabole sont tournées vers le haut, donc le signe de a est positif
- La courbe est décroissante sur ]-inf ; -b/2a] et croissante sur [-b/2a ; +inf[ donc le discriminant est négatif sur ]-inf ; -b/2a] et positif sur [-b/2a ; +inf[
- f n’a pas de racine, donc f est strictement positive partout
Tableau de signe de f

Courbe 6 :
- Les branches de la parabole sont tournées vers le bas, donc le signe de a est négatif
- La courbe est croissante sur ]-inf ; -b/2a] et décroissante sur [-b/2a ; +inf[ donc le discriminant est positif sur ]-inf ; -b/2a] et négatif sur [-b/2a ; +inf[
- f n’a pas de racine, donc f est strictement négative partout
Tableau de signe de f

3.b.
- Si le polynôme f a deux racines :
f est du signe opposé de a entre ses racines et du signe de a en dehors de ses racines
- Si le polynôme f a une ou zéro racine :
f est du signe de a partout

Le 01 janvier 2024 à 23:00:22 :

cos(2a) = cos²(a) - sin²(a)
=> cos²(a) = cos(2a) + sin²(a)
=> cos²(a) + cos²(a) = cos(2a) + sin²(a) + cos²(a)
=> 2*cos²(a) = cos²(a) + sin²(a) + cos(2a)
(rappel : pour tout réel a, cos²(a) + sin²(a) = 1)
=> 2*cos²(a) = 1 + cos(2a)
=> cos²(a) = (1 + cos(2a))/2

f admet -1 et 3 pour racines, donc il existe un réel a tel que, pour tout réel x
f(x) = a*(x + 1)*(x - 3)

f(0) = -3
=> -3 = a*(0 + 1)*(0 - 3)
=> -3 = a*1*(-3)
=> -3 = a*(-3)
=> a = -3/-3 = 1

La forme factorisée de f est
f(x) = (x + 1)*(x - 3)

La forme développée de f est
f(x) = x² + x - 3x - 3 = x² - 2x - 3

Le 09 janvier 2024 à 19:36:00 :

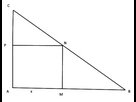
1.a.
[AM] est un segment dont la longueur est inférieure ou égale à celle du segment [AB]
x = AM se trouve dans [0 ; 6]

1.b.
AMNP est un rectangle, son aire est égale au produit de sa longueur et de sa largeur
A(x) = AM*MN = x*MN

Calcul de la longueur MN :
Les points AMB sont alignés
Les points APC sont alignés
Les segments [MN] et [AC] sont parallèles
Donc d’après le théorème de Thalès
MN/AC = BM/BA
=> MN/6 = (6 - x)/6
=> MN = 6 - x

A(x) = x*(6 - x) = -x^2 + 6x

2.
A(x) >= 8
=> -x^2 + 6x >= 8
=> -x^2 + 6x - 8 >= 0

Étude du polynôme -x^2 + 6x - 8
Calcul du discriminant
Delta = 6^2 - 4*(-1)*(-8) = 36 - 32 = 4 > 0
Ce polynôme a deux racines réelles qu’on note x1 et x2
Le coefficient dominant de ce polynôme est -1 qui est < 0, donc il est positif entre ses racines et négatif ailleurs.
Calcul des racines
x1 = (-6 - racine(4))/(2*(-1)) = (-6 - 2)/(-2) = (-8)/(-2) = 8/2 = 4
x1 est dans [0 ; 6]
x2 = (-6 + racine(4))/(2*(-1)) = (-6 + 2)/(-2) = (-4)/(-2) = 4/2 = 2
x2 est dans [0 ; 6]

A(x) >= 8
=> x se trouve dans [2 ; 4]
=> La longueur du segment [AM] se trouve dans [2 ; 4]

3.
L’aire d’un triangle rectangle est égale à la moitié du produit des longueurs de l’angle droit
On note At l’aire du triangle ABC
At = AB*AC/2
ABC étant isocèle rectangle on a
At = AB^2/2 = 6^2/2 = 36/2 = 18

A(x) <= (1/4)*At
=> A(x) - (1/4)*At <= 0
=> -x^2 + 6x - (1/4)*18 <= 0
=> -x^2 - 6x - 9/2 <= 0

Étude du polynôme -x^2 + 6x - 9/2
Calcul du discriminant
Delta = 6^2 - 4*(-1)*(-9/2) = 36 - 18 = 18 > 0
Ce polynôme a deux racines réelles qu’on note x1 et x2
Le coefficient dominant de ce polynôme est -1 < 0, donc il est positif entre ses racines et négatif ailleurs.
Calcul des racines
(racine(18) = racine(9*2) = racine(9)*racine(2) = 3*racine(2))
x1 = (-6 - racine(18))/(2*(-1)) = (-6 - 3*racine(2))/(-2) = 3 + (3/2)*racine(2) = 5,12 à 10^-2 près
x1 est dans [0 ; 6]
x2 = (-6 + racine(18))/(2*(-1)) = (-6 + 3*racine(2))/(-2) = 3 - (3/2)*racine(2) = 0,88 à 10^-2 près
x2 est dans [0 ; 6]

A(x) <= (1/4)*At
=> x se trouve dans [0 ; 3 - (3/2)*racine(2)] ou x se trouve dans [3 + (3/2)*racine(2) ; 6]
=> la longueur de [AM] se trouve dans [0 ; 3 - (3/2)*racine(2)] ou la longueur de [AM] se trouve dans [3 + (3/2)*racine(2) ; 6]

4.
(abs(x) = valeur absolue de x)
A(x) = -x^2 + 6x
= -x^2 + 2*x*2 - 3^2 + 3^2
= -(x^2 - 2*3*x + 3^2) + 3^2
= -(x - 3)^2 + 3^2
= -(x - 3)^2 + 9

Avec cette forme canonique on a :
- Le coefficient dominant du polynôme qui est -1
- Les coordonnées du sommet qui sont (3 ; 9)
A est croissante sur [0 ; 3] et décroissante sur [3 ; 6]
A(0) = -0^2 + 6*0 = 0
A(6) = -6^2 + 6*6 = 6^2 - 6^2 = 0

Tableau de variations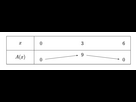

5.
A(x) est maximale en son sommet c’est à dire pour x = 3
=> Le segment [AM] est de longueur 3

AM*MN = A(3)
=> 3*MN = 9
=> MN = 9/3 = 3

Le rectangle AMNP a les côtés égaux, donc c’est un carré

Le 16 janvier 2024 à 21:26:51 :

AYAAAAAAAAAAAAAAA
ta post

Tu fais vraiment tous les dms tout seul où tu demandes à chatgépété ?

Le 16 janvier 2024 à 21:26:51 :

1.a)
Les points CEB sont alignés
Les points ADB sont alignés
Les droites (AC) et (DE) sont parallèles
D’après le théorèmes de Thalès
ED/AC = BD/AB
=> ED = AC*BD/AB = 1,5x/4

1.b)
L’aire d’un rectangle est égale à sa longueur multipliée par sa largeur
A(x) = AD*ED

AD = AB - BD = 4 - x
A(x) = AD*ED = (4 - x)*1,5x/4 = 1,5*(-x² + 4x)/4

2.a)
A(2) = (4 - 2)*1,5*2/4 = 2*3/4 = 3/2

A(x) = 1,5*( = (4 - x)*3x/8 = 3*(-x² + 4x)/8
A(2) = 3/2 = 3*4/8

A(x) - A(2) = 3*(4x - x²)/8 - 3*4/8 = 3*(-x² + 4x - 4)/8 = -3*(x² - 4x + 4)/8 = -3*(x² - 2*x*2 + 2²)/8 = -3*(x - 2)²/8

2.b)
Pour tout x dans [0 ; 4]
(x - 2)² >= 0
=> 3*(x - 2)²/ 8 >= 0
=> -3*(x - 2)²/8 <= 0
=> A(x) - A(2) <= 0
=> A(x) <= A(2)

Ça valide la conjecture de Cyrielle, l’aire A(x) est maximum pour x = 2.
La baie vitrée apporte le maximum de lumière lorsque AD = 4 - x = 4 - 2 = 2 m et DE = 1,5x/4 = 1,5*2/4 = 1,5/2 = 0,75 m.

Le 16 janvier 2024 à 21:30:28 :
Tu fais vraiment tous les dms tout seul où tu demandes à chatgépété ?

Je n'ai pas besoin d'aide pour traiter les devoirs qui sont postés ici.