Juste la 2.c et la 2.d s'il te plaît. 
Sujet :
Je fais vos DM de maths Collège/Lycée
Le 22 avril 2024 à 12:17:02 :
Juste la 2.c et la 2.d s'il te plaît.
2.c.
f(t+1)/f(t)
= (5000*exp(0,0075(x+1)))/(5000*exp(0,0075x))
= exp(0,0075(x+1))/exp(0,0075x)
= (exp(0,0075x + 0,0075)*exp(0,0075))/exp(0,0075x)
= (exp(0,0075x)*exp(0,0075))/exp(0,0075x)
= exp(0,0075)
L’ajustement de la suite (un) est une suite géométrique de raison exp(0,0075)
2.d.
f(t) >= 22950
<=> 5000*exp(0,0075t) >= 22950
Si tu as vu la fonction ln
<=> exp(0,0075t) >= 22950/5000
<=> ln(exp(0,0075t) >= ln(22950/5000)
<=> 0,0075t >= ln(22950/5000)
<=> t >= ln(22950/5000)/0,0075
ln(22950/5000)/0,0075 = 203,2 à 10^-1 près donc au bout de 204 ans.
Si tu n’as pas vu la fonction ln
Tu rentres f(x) = 5000*exp(0,0075x) dans la calculatrice et tu regardes à partir de quel entier tu dépasses 22950
Tu devrais trouver f(203) = 22918 < 22950 et f(204) = 23090 >= 22950 donc à partir de 204 ans
Juste la 2.d 
Merci pour ton aide !
Le 23 avril 2024 à 12:40:27 :
Juste la 2.d
Merci pour ton aide !
2.b ?
L'algo retourne la première valeur de x au dessus de 0 pour laquelle exp(x) >= k arrondi à 10^-1 près.
Le 23 avril 2024 à 12:49:18 :
Le 23 avril 2024 à 12:40:27 :
Juste la 2.d
Merci pour ton aide !2.b ?
L'algo retourne la première valeur de x au dessus de 0 pour laquelle exp(x) >= k arrondi à 10^-1 près.
À partir de 0 plutôt*
Le 23 avril 2024 à 16:59:47 :
salut voici mon DM
merci d'avance mec !
Exercice 1
1. f’(x) = -8x^2 - 1 - x
2. g’(x) = (9/2)*x + 5 - 6x^2 - 3/2
3. h’(x) = 3
4. Une fonction affine est de la forme f(x) = ax + b, où a est le coefficient directeur et b l’ordonnée à l’origine qui sont tous deux des nombres réels.
f’(x) = a donc la dérivée d’une fonction affine est égale à son coefficient directeur.
Exercice 2
Partie A
1. D’après le graphique, pour 5 pièces produites par jour le montant des charges s’élève à environ 1500€
2. D’après le graphique, pour un montant des charges de 2000€ on produit environ 9 pièces par jour.
---
1. Lorsque l’entreprise fabrique exactement 5 pièces, la courbe du chiffre d’affaire est en dessous de celle des charges, donc l’entreprise n’est pas bénéficiaire.
Lorsque l’entreprise fabrique exactement 14 pièces, la courbe du chiffre d’affaire est au dessus de celle des charges, donc l’entreprise est bénéficiaire.
2. Graphiquement, on peut estimer qu’il faudrait fabriquer environ 17 pièces par jour pour que le bénéfice soit maximal.
Pour 17 pièces, on a un chiffre d’affaires d’environ 4250€ pour 3200€ de charges, le bénéfice maximal serait d’environ 4250 - 3200 = 1050€
3. L’entreprise réalise un bénéfice positif lorsque la courbe du chiffre d’affaire est au dessus de la courbe des charges.
Ce qui correspond environ à un nombre de pièces par jour se trouvant dans l’intervalle [8 ; 23]
Partie B
1. B’(x) = -3x^2 + 60x - 153
2. -3(x - 3)(x - 17) = -3(x^2 - 3x - 17x + 51) = -3(x^2 - 20x + 51) = -3x^2 + 60x - 153 = B’(x)
3. x - 3 = 0 <=> x = 3
x - 17 = 0 <=> x = 17
On en déduit le tableau de signes de B’
4. B(0) = -100
B(3) = -316
B(17) = 1056
B(25) = -800
On en déduit le tableau de variations complet de B
5. D’après le tableau de variations, le nombre de pièces que l’entreprise doit produire chaque jour pour que le bénéfice réalisé soit maximal est de 17.
6. Le bénéfice maximal vaut 1056€
Ah merci
yo khey , t'a l'air de te débrouiller en maths , j'ai pas de dm mais j'ai besoin d'aide a vrai dire , j'suis en premiere et je change de spé pour passer en maths sauf que ducoup j'ai aucun notion a part les suites aritmetiques/geometriques
tu pourrais me donner les notions de base pour que je puisse me mettre a niveau stp ? 
merci khey
Le 23 avril 2024 à 23:58:40 :
yo khey , t'a l'air de te débrouiller en maths , j'ai pas de dm mais j'ai besoin d'aide a vrai dire , j'suis en premiere et je change de spé pour passer en maths sauf que ducoup j'ai aucun notion a part les suites aritmetiques/geometriquestu pourrais me donner les notions de base pour que je puisse me mettre a niveau stp ?
merci khey
En Avril t'as changé de spé ?
Le 23 avril 2024 à 12:49:18 :
Le 23 avril 2024 à 12:40:27 :
Juste la 2.d
Merci pour ton aide !2.b ?
L'algo retourne la première valeur de x au dessus de 0 pour laquelle exp(x) >= k arrondi à 10^-1 près.
3.d plutôt, désolé
Le 24 avril 2024 à 00:10:27 :
Le 23 avril 2024 à 12:49:18 :
Le 23 avril 2024 à 12:40:27 :
Juste la 2.d
Merci pour ton aide !2.b ?
L'algo retourne la première valeur de x au dessus de 0 pour laquelle exp(x) >= k arrondi à 10^-1 près.3.d plutôt, désolé
3.b ?
pour resol2 j'ai cette fonction :
def resol2(k,p):
x=0
while(exp(x)<k):
x=x+p
return x+p
Et pour arrondir par défaut, j'enlève le +p dans le return
def resol2(k,p):
x=0
while(exp(x)<k):
x=x+p
return x
Le 23 avril 2024 à 23:58:40 :
yo khey , t'a l'air de te débrouiller en maths , j'ai pas de dm mais j'ai besoin d'aide a vrai dire , j'suis en premiere et je change de spé pour passer en maths sauf que ducoup j'ai aucun notion a part les suites aritmetiques/geometriquestu pourrais me donner les notions de base pour que je puisse me mettre a niveau stp ?
merci khey
Je ne sais pas trop comment ça se passe au niveau des spé au lycée car je ne me suis pas renseigné sur la réforme.
Si tu penses être capable de bosser seul, il y a des ressources sur le net pour préparer la première et la terminale
Première : https://www.maths-et-tiques.fr/index.php/prep1 (qui revoit les notions de seconde)
Terminale : https://www.maths-et-tiques.fr/index.php/1s-ts (qui revoit les notions de première)
Sinon le mieux c'est de prendre un prof particulier
Voilà mon DM pour que tu le résout s'il te plaît (Pour ce soir si possible ?) 
1er exercice
Salmia, une jeune ingénieure, fabrique des tablettes numériques et souhaite prendre le statut d'auto-entrepreneure pour les commercialiser. Elle estime qu'elle peut en fabriquer au maximum 50 par mois. Les coûts de fabrication, en euro, sont modélisés par
la fonction C définie sur l'intervalle [0:50] par:
C(x)=x²+200+1056
oùs représente le nombre de tablettes produites et vendues.
Chaque tablette est vendue 220 €
1. Justifier que les recettes sont données, en euro, par la fonction R définie sur [0:50] par R(x)=220x.
2. Obtenir les courbes des fonctions C'et R sur une calculatrice et déterminer graphiquement le nombre minimal de tablettes que Samia doit produire et vendre mensuellement pour gagner de l'argent.
3. On note B la fonction bénéfice, c'est-à-dire la fonction définie sur [0:50] par B(x) = R(x)-Cx).
a. Justifier que pour tout réelx de l'intervalle [0; 50]: B(x)=x²+20x-1056.
b. Vérifier que pour tout réel x de l'intervalle [0:50]: B(x)=(x+44)(x-24).
c. Dresser le tableau de signes de l'expression B(x).
d. Ce tableau est-il cohérent avec la réponse apportée à la question 2.? Justifier.
2nd exercice
La vitesse v exprimée en km-h, d'un satellite artificiel toumant autour de la Terre à l'altitude h, exprimée en km, est donnée par:
. . . . . . . . . 356 R
v= ____________________________
(racine carrée au dessus)R+h
où R est le rayon de la Terre (R-6370 km).
1. Si le satellite se déplace à 7 573 km/h(esxposant -1), quelle est son altitude? On arrondira au kilomètre.
2. Un satellite géostationnaire se trouve à 35 786 km d'altitude.
a. Quelle est sa vitesse? Arrondir au km/h(exposant -1).
b. Quelle est sa période de révolution autour de la Terre?
PISTE: 2.b. Calculer la distance parcourue par le satellite pendant un tour, en admettant que son orbite décrit un cercle dont le centre est le centre de la Terre.
Le 28 avril 2024 à 15:35:25 :
Voilà mon DM pour que tu le résout s'il te plaît (Pour ce soir si possible ?)
1er exercice
Salmia, une jeune ingénieure, fabrique des tablettes numériques et souhaite prendre le statut d'auto-entrepreneure pour les commercialiser. Elle estime qu'elle peut en fabriquer au maximum 50 par mois. Les coûts de fabrication, en euro, sont modélisés par
la fonction C définie sur l'intervalle [0:50] par:
C(x)=x²+200+1056
oùs représente le nombre de tablettes produites et vendues.
Chaque tablette est vendue 220 €
1. Justifier que les recettes sont données, en euro, par la fonction R définie sur [0:50] par R(x)=220x.
2. Obtenir les courbes des fonctions C'et R sur une calculatrice et déterminer graphiquement le nombre minimal de tablettes que Samia doit produire et vendre mensuellement pour gagner de l'argent.
3. On note B la fonction bénéfice, c'est-à-dire la fonction définie sur [0:50] par B(x) = R(x)-Cx).
a. Justifier que pour tout réelx de l'intervalle [0; 50]: B(x)=x²+20x-1056.
b. Vérifier que pour tout réel x de l'intervalle [0:50]: B(x)=(x+44)(x-24).
c. Dresser le tableau de signes de l'expression B(x).
d. Ce tableau est-il cohérent avec la réponse apportée à la question 2.? Justifier.
2nd exercice
La vitesse v exprimée en km-h, d'un satellite artificiel toumant autour de la Terre à l'altitude h, exprimée en km, est donnée par:
. . . . . . . . . 356 R
v= ____________________________
(racine carrée au dessus)R+h
où R est le rayon de la Terre (R-6370 km).
1. Si le satellite se déplace à 7 573 km/h(esxposant -1), quelle est son altitude? On arrondira au kilomètre.
2. Un satellite géostationnaire se trouve à 35 786 km d'altitude.
a. Quelle est sa vitesse? Arrondir au km/h(exposant -1).
b. Quelle est sa période de révolution autour de la Terre?
PISTE: 2.b. Calculer la distance parcourue par le satellite pendant un tour, en admettant que son orbite décrit un cercle dont le centre est le centre de la Terre.
Je veux bien faire ton devoir mais il y a au moins une erreur dans l'énoncé (la fonction C(x) de l'exercice 1 ne me semble pas juste)
Relis ce que tu as posté et corrige les fautes
Le 28 avril 2024 à 16:40:28 :
Le 28 avril 2024 à 15:35:25 :
Voilà mon DM pour que tu le résout s'il te plaît (Pour ce soir si possible ?)
1er exercice
Salmia, une jeune ingénieure, fabrique des tablettes numériques et souhaite prendre le statut d'auto-entrepreneure pour les commercialiser. Elle estime qu'elle peut en fabriquer au maximum 50 par mois. Les coûts de fabrication, en euro, sont modélisés par
la fonction C définie sur l'intervalle [0:50] par:
C(x)=x²+200+1056
oùs représente le nombre de tablettes produites et vendues.
Chaque tablette est vendue 220 €
1. Justifier que les recettes sont données, en euro, par la fonction R définie sur [0:50] par R(x)=220x.
2. Obtenir les courbes des fonctions C'et R sur une calculatrice et déterminer graphiquement le nombre minimal de tablettes que Samia doit produire et vendre mensuellement pour gagner de l'argent.
3. On note B la fonction bénéfice, c'est-à-dire la fonction définie sur [0:50] par B(x) = R(x)-Cx).
a. Justifier que pour tout réelx de l'intervalle [0; 50]: B(x)=x²+20x-1056.
b. Vérifier que pour tout réel x de l'intervalle [0:50]: B(x)=(x+44)(x-24).
c. Dresser le tableau de signes de l'expression B(x).
d. Ce tableau est-il cohérent avec la réponse apportée à la question 2.? Justifier.
2nd exercice
La vitesse v exprimée en km-h, d'un satellite artificiel toumant autour de la Terre à l'altitude h, exprimée en km, est donnée par:
. . . . . . . . . 356 R
v= ____________________________
(racine carrée au dessus)R+h
où R est le rayon de la Terre (R-6370 km).
1. Si le satellite se déplace à 7 573 km/h(esxposant -1), quelle est son altitude? On arrondira au kilomètre.
2. Un satellite géostationnaire se trouve à 35 786 km d'altitude.
a. Quelle est sa vitesse? Arrondir au km/h(exposant -1).
b. Quelle est sa période de révolution autour de la Terre?
PISTE: 2.b. Calculer la distance parcourue par le satellite pendant un tour, en admettant que son orbite décrit un cercle dont le centre est le centre de la Terre.Je veux bien faire ton devoir mais il y a au moins une erreur dans l'énoncé (la fonction C(x) de l'exercice 1 ne me semble pas juste)
Relis ce que tu as posté et corrige les fautes
Oui tu as raison la fonction C(x) est -x²+200x+1056
Je vais copier coller et corriger tout j'arrive
Le 28 avril 2024 à 17:42:52 :
1er exercice
Salmia, une jeune ingénieure, fabrique des tablettes numériques et souhaite prendre le statut d'auto-entrepreneure pour les commercialiser. Elle estime qu'elle peut en fabriquer au maximum 50 par mois. Les coûts de fabrication, en euro, sont modélisés par
la fonction C définie sur l'intervalle [0:50] par:
C(x)=-x²+200x+1056
oùs représente le nombre de tablettes produites et vendues.
Chaque tablette est vendue 220 €
1. Justifier que les recettes sont données, en euro, par la fonction R définie sur [0;50] par R(x)=220x.
2. Obtenir les courbes des fonctions C'et R sur une calculatrice et déterminer graphiquement le nombre minimal de tablettes que Samia doit produire et vendre mensuellement pour gagner de l'argent.
3. On note B la fonction bénéfice, c'est-à-dire la fonction définie sur [0:50] par B(x) = R(x) =C(x).
a. Justifier que pour tout réelx de l'intervalle [0; 50]: B(x)=x²+20x-1056.
b. Vérifier que pour tout réel x de l'intervalle [0:50]: B(x)=(x+44)(x-24).
c. Dresser le tableau de signes de l'expression B(x).
d. Ce tableau est-il cohérent avec la réponse apportée à la question 2.? Justifier.
2nd exercice
La vitesse v exprimée en km/h, d'un satellite artificiel toumant autour de la Terre à l'altitude h, exprimée en km, est donnée par:
. . . . . . 356 R
v= ______________________
(racine carrée)R+h
où R est le rayon de la Terre (R=6370 km).
1. Si le satellite se déplace à 7 573 km/h(exposant -1), quelle est son altitude? On arrondira au kilomètre.
2. Un satellite géostationnaire se trouve à 35 786 km d'altitude.
a. Quelle est sa vitesse? Arrondir au km/h(exposant -1).
b. Quelle est sa période de révolution autour de la Terre?
PISTE: 2.b. Calculer la distance parcourue par le satellite pendant un tour, en admettant que son orbite décrit un cercle dont le centre est le centre de la Terre.
Exercice 1
1. Chaque tablette est vendue 220€, par conséquent, si elle vend x tablette, sa recette sera de 220x €.
Donc R(x) = 220x.
2. Pour que Samia gagne de l’argent il faut que la recette de sa vente de tablette R soit plus élevée que son coût de production C.
Graphiquement, ça signifie que la courbe représentative de R soit au dessus de la courbe représentative de R.
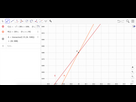
Sur geogebra on observe que la courbe représentative de R est en dessous de celle de C jusqu’à leur point d’intersection puis au dessus.
Les coordonnées du point d’intersection sont (24 ; 5280)
Par conséquent, Samia doit produire et vendre mensuellement plus de 24 tablettes pour gagner de l’argent.
3.a. B(x) = R(x) - C(x)
B(x) = 220x - (-x^2 + 200x + 1056) = 220x + x^2 - 200x - 1056 = x^2 + 20x - 1056
3.b. On développe (x + 44)(x - 24)
(x + 44)(x - 24) = x^2 + 44x - 24x - 1056 = x^2 + 20x - 1056 = B(x)
3.c. x + 44 = 0 <=> x = -44
x - 24 = 0 <=> x = 24
On en déduit le tableau de signe de B
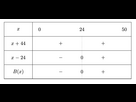
3.d. Le bénéfice est négatif lorsqu’on vend moins de 24 tablettes et le bénéfice est positif lorsqu’on vend plus de 24 tablettes. Ce qui est cohérent avec ce qui a été observé par la lecture graphique de la question 2.
Exercice 2
1. v = 356*R/racine(R + h)
<=> v*racine(R + h) = 356*R
<=> racine(R + h) = 356*R/v
<=> R + h = (356*R/v)² (car R et v sont positifs)
<=> h = (356*R/v)² - R
Pour un déplacement v = 7573 km/h et un rayon de la terre R = 6370 km on a alors
h = (356*6370/7573)² - 6370 = 83299 km arrondi au km près.
2.a. Il suffit de remplacer dans la formule de base R = 6370 km et h = 35786 km
v = 356*6370/racine(6370 + 35786) = 2267720/racine(42156) = 11045 km arrondi au km près.
2.b. Vitesse parcourue par le satellite pendant un tour :
v = 2pi*(R + h)/T où T est la période de révolution autour de la terre en h
<=> v*T = 2pi*(R + h)
<=> T = 2pi*(R + h)/v
Pour une vitesse d’environ 11045 km on a alors
T = 2pi*(6370 + 35786)/11045 = 2pi*42156/11045 = 24h arrondi à l’heure près.
Merci beaucoup
Sujet :
Je fais vos DM de maths Collège/Lycée