Blabla 15-18 ans

Le 11 septembre 2022 à 15:46:01 :

Salut, j'ai fait le plus simple

1) a)
g(x) = x²+2x-4
a=1, b=2, c=-4

On pose Delta = b²-4ac = 2²-4*1*(-4)=20
Delta>0 donc il y a 2 solutions :

X1=(-b+racine carré(Delta)) / (2a) = (-2+racinecarré(20))/2 soit environ 1.24
X2=(-b-racine carré(Delta)) / (2a) = (-2-racinecarré(20))/2 soit environ -3.24

b) Par lecture graphique : (fais-le au crayon)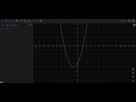

La courbe se situe au-dessus de l’axe des abscisses sur les intervalles [-infini ; X2] et [X1 ; +infini] . Sur ces intervalles, la fonction g est donc positive.
Par ailleurs, la fonction g est négative sur l’intervalle [X2;X1] .
On peut donc dresser le tableau de signes suivant :

Normalement, t'as compris ça ?

Le 11 septembre 2022 à 18:15:51 :

Le 11 septembre 2022 à 15:46:01 :

Salut, j'ai fait le plus simple

1) a)
g(x) = x²+2x-4
a=1, b=2, c=-4

On pose Delta = b²-4ac = 2²-4*1*(-4)=20
Delta>0 donc il y a 2 solutions :

X1=(-b+racine carré(Delta)) / (2a) = (-2+racinecarré(20))/2 soit environ 1.24
X2=(-b-racine carré(Delta)) / (2a) = (-2-racinecarré(20))/2 soit environ -3.24

b) Par lecture graphique : (fais-le au crayon)

La courbe se situe au-dessus de l’axe des abscisses sur les intervalles [-infini ; X2] et [X1 ; +infini] . Sur ces intervalles, la fonction g est donc positive.
Par ailleurs, la fonction g est négative sur l’intervalle [X2;X1] .
On peut donc dresser le tableau de signes suivant :

Normalement, t'as compris ça ?

Merci beaucoup
Je me doutais bien qu'il fallait utiliser le discriminant, mais j'en étais pas sûr
T'as pas réussi à faire le reste toi non plus ?

Je suis en train d'essayer, je te re-dis quoi dans 1 heure : )

Le 11 septembre 2022 à 18:34:30 :
Je suis en train d'essayer, je te re-dis quoi dans 1 heure : )

Merci beaucoup

Bon, quelques indices :
2)a) (x²-4)*e(x) est sous la forme u*v avec u =(x²-4) et v = e(x)
Dérivé de u*v = u(x)*v'(x) + u'(x)*v(x)

La dérivé de e(x) est égale à elle-même donc e(x)
(x²-4)*e(x)’+ (x²-4)’*e(x) = (x²-4)*e(x)+ 2x*e(x)
On factorise avec e(x) :
e(x) * ( (x²-4) + 2x ) = e(x) * (x²+2x-4) = e(x) * g(x)

b) On a f’(x) = e(x)*g(x)
Puisque e(x) est positif , f’(x) aura le même tableau de signe que g(x)
C’est comme avec les multiplications : - *+ = - : c’est toujours le moins qui influence. Ici e(x) est + donc le signe sera en fonction de g(x)

c) Le tableau de variation, c'est avec la dérivée, il me semble ?
f'(x) = (x²+2x-4)*e(x)
D’abord, on résout l’équation suivante : (x²+2x-4)*e(x) = 0
- Si e(x) = 0 alors : (x²+2x-4)*e(x) = 0 mais il n’existe pas de valeur telle que e(x) = 0, e(x) tend vers 0 mais ne l’atteint jamais !
- Si (x²+2x-4) = 0 alors : (x²+2x-4)*e(x) = 0
-> donc x=X2 ou x=X1 comme dans le 1)
et faut faire le tableau avec la dérivée

d) Un maximum local c’est juste la valeur la plus haute en ordonnée.

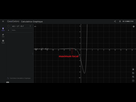
Pour justifier je m'en rappelle plus, pareil pour la e , je regarderais peut être ce soir

Le 11 septembre 2022 à 19:48:06 :
Bon, quelques indices :
2)a) (x²-4)*e(x) est sous la forme u*v avec u =(x²-4) et v = e(x)
Dérivé de u*v = u(x)*v'(x) + u'(x)*v(x)

La dérivé de e(x) est égale à elle-même donc e(x)
(x²-4)*e(x)’+ (x²-4)’*e(x) = (x²-4)*e(x)+ 2x*e(x)
On factorise avec e(x) :
e(x) * ( (x²-4) + 2x ) = e(x) * (x²+2x-4) = e(x) * g(x)

b) On a f’(x) = e(x)*g(x)
Puisque e(x) est positif , f’(x) aura le même tableau de signe que g(x)
C’est comme avec les multiplications : - *+ = - : c’est toujours le moins qui influence. Ici e(x) est + donc le signe sera en fonction de g(x)

c) Le tableau de variation, c'est avec la dérivée, il me semble ?
f'(x) = (x²+2x-4)*e(x)
D’abord, on résout l’équation suivante : (x²+2x-4)*e(x) = 0
- Si e(x) = 0 alors : (x²+2x-4)*e(x) = 0 mais il n’existe pas de valeur telle que e(x) = 0, e(x) tend vers 0 mais ne l’atteint jamais !
- Si (x²+2x-4) = 0 alors : (x²+2x-4)*e(x) = 0
-> donc x=X2 ou x=X1 comme dans le 1)
et faut faire le tableau avec la dérivée

d) Un maximum local c’est juste la valeur la plus haute en ordonnée.

Pour justifier je m'en rappelle plus, pareil pour la e , je regarderais peut être ce soir

Le 11 septembre 2022 à 15:46:01 :

1.
a)
Calcul du discriminant
Delta = 2^2 - 4*1*(-4) = 4 + 16 = 20
Delta > 0, g admet deux racines réelles, qu'on notera x1 et x2
x1 = (-2 - racine(20))/(2*1) = (-2 - racine(20))/2 = -3,24 à 10^-2 près
x2 = (-2 - racine(20))/(2*1) = (-2 + racine(20))/2 = 1,24 à 10^-2 près

1.
b)
Le coefficient du terme de degré 2 (ici x^2 = 1.x^2) est 1 qui est positif ce qui implique que g est négative entre ses racines et positive ailleurs, c'est à dire
g est positive sur ]-infini ; x1]
g est négative sur [x1 ; x2]
g est positive sur [x2 ; +infini[

2.
a)
f'(x) = (x^2 - 4)'.exp(x) + (x^2 - 4).exp(x)' = 2x.exp(x) + (x^2 - 4).exp(x) = (x^2 + 2x - 4).exp(x) = g(x).exp(x)

2.
b)
La fonction exp est positive, par conséquent f' est du même signe que g

2.
c)
Étudier la variation de f revient à étudier le signe de sa dérivée, qui est du même signe que g
En reprenant ce qu'on a vu dans la question 1.b) on a
f' est positive sur ]-infini ; x1] alors f est croissante sur cet intervalle
f' est négative sur [x1 ; x2] alors f est décroissante sur cet intervalle
f' est positive sur [x2 ; +infini[ alors f est croissante sur cet intervalle

2.
d)
f est croissante sur ]-infini ; x1]
f est décroissante sur [x1 ; 0]
Par conséquent, f admet un maximum local en x1 qui vaut f(x1) = 0.25 à 10^-2 près

2.
e)
L'équation de la tangente de la fonction f au point d'abscisse a est Ta(x) = f(a) - f'(a).(x - a)
Au point d'abscisse 1 on a alors
T1(x) = f(1) - f'(1).(x - 1) = -3.exp(1) - (-1).exp(1).(x - 1) = -3.exp(1) + (x - 1).exp(1) = (x - 1 - 3).exp(1) = (x - 4).exp(1)

Merci

Je suis bloqué sur cet exercice

Le 12 septembre 2022 à 21:04:30 :

Je suis bloqué sur cet exercice

1.
a)
En 2020 on a 1000 ha
En 2021 on perd 2% de ce qu'on avait en 2020 et on ajoute 100 ha, ce qui nous donne U1 = 1000*0,98 + 100 = 1080 ha
En 2022 on perd 2% de ce qu'on avait en 2021 et on ajoute 100 ha, ce qui nous donne U2 = 1080*0,98 + 100 = 1158,4 ha

1.
b)
Si Un est une suite arithmétique, alors on a U1 - U0 = U2 - U1
or, U1 - U0 = 1080 - 1000 = 80 et U2 - U1 = 1158,4 - 1080 = 78,4
Donc Un n'est pas une suite arithmétique
Si Un est une suite géométrique alors U1/U0 = U2/U1
or, U1/U0 = 1080/1000 = 0,08 et U2/U1 = 1,07 à 10^-2 près
Donc Un n'est pas une suite géométrique

1.
c)
Un est la surface boisée en ha après n années
L'année n+1, on perd 2% de la surface de l'année n et on ajoute 100 ha, ce qui veut dire qu'on a alors Un+1 = 0,98*Un + 100

2.
a)
Ce que tu as écrit est juste

2.
b)
En 15 années

3.
a)
On va montrer que Vn+1 = Vn*0,98
Vn+1 = Un+1 - 5000 = 0,98*Un + 100 - 5000 = 0,98*Un - 4900 = 0,98*Un + 0,98*5000 = (Un + 5000)*0,98 = Vn*0,98

3.
b)
V0 = U0 - 5000 = 1000 - 5000 = -4000

3.
c)
Vn est une suite géométrique de raison 0,98 par conséquent Vn = V0*0,98^n = -4000*0,98^n

3.
d)
Vn = Un - 5000 donc Un = Vn + 5000 = -4000*0,98^n + 5000

Le 23 septembre 2022 à 14:49:46 :

Partie A

1.
g’(x) = -3/x^2 - 1/x = (-x - 3)/x^2

2.
Sur ]0 ;+inf[, -x - 3 < 0 et x^2 > 0, donc g’ < 0 pour tout x dans ]0 ;+inf[
Par conséquent, g est décroissante sur ]0 ;+inf[

3.
g(1) = 3/1 - 1 - ln(1) = 3 - 1 - 0 = 2
g(2) = 3/2 - 1 - ln(2) = 1/2 - ln(2) = -0.19 à 10^(-2) près
g est une fonction continue et décroissante sur [1 ;2]
0 est dans l’intervalle [g(2) ; g(1)]
Donc il existe une unique alpha tel que g(alpha) = 0
alpha = 1,86 à 10^(-2) près.

Partie B

1.
f’(x) = (-x + 3)’.ln(x) + (-x + 3).ln’(x) = -ln(x) + (-x + 3)/x = 3/x - 1 - ln(x) = g(x)

2.
D’après la partie 2, on sait que g est décroissante sur ]0 ; +inf[ et qu’elle s’annule en alpha.
Par conséquent,
g est positive sur ]0 ; alpha] donc f est croissante sur ]0 ; alpha]
g est négative sur [alpha ; +inf[ => f est décroissante sur [alpha ; +inf[

3.
h’(x) = (2x - 3)’.ln(x) + (2x - 3).ln’(x) = 2.ln(x) + (2x - 3)/x = -3/x + 2 + 2.ln(x)
h’’(x) = 3/x^2 + 2/x = (3 + 2x)/x
3 + 2x > 0 sur ]0 ; +inf[ et x > 0 sur ]0 ; +inf[ donc h’’ > 0 sur ]0 ; +inf[ => h’ est croissante sur ]0 ; +inf[
h’(1) = -3/1 + 2 + 2.ln(1) = -1
h’(2) = -3/2 + 2 + 2.ln(2) = 1.89 à 10^(-2) près
h’ est croissante et continue sur ]0 ; +inf[ et 0 est dans l’intervalle [h’(1) ; h’(2)] donc il existe un unique alpha’ dans ]0 ; +inf[ tel que h’(alpha’) = 0
alpha’ = 1,24 à 10^(-2) près
Ce qui implique que
h’ est négative sur ]0 ; alpha’] donc h est décroissante sur ]0 ; alpha’]
h’ est positive sur [alpha’ ; +inf[ donc h est croissante sur [alpha ; +inf[

tu peux faire un exo de physique chimie stp , j'suis en première
on revoit avec la prof les bases de la seconde, et récAp de tout les exos de 2nd...

Le 02 octobre 2022 à 16:49:35 :

Exercice 1 :

A = (racine(2) + 2*racine(3))^2 = racine(2)^2 + 2*racine(2)*2*racine(3) + racine(3)^2 = 2 + 4*racine(6) + 3 = 4*racine(6) + 5
A est un nombre irrationnel, il appartient à l’ensemble R

6*10^4*5*10^-2 = 6*5*10^(4-2) = 30*10^2
(-2*10^-1)^3 = (-2)^3*(10^-1)^3 = -8*10^-3
B = (6*10^4*5*10^-2)/(-2*10^-1)3 = (30*10^2)/(-8*10^-3) = 30/(-8*10) = -3/8
B est un nombre rationnel, il appartient à l’ensemble Q (et aussi à l’ensemble R)

2 + 1/4 = 8/4 + 1/4 = 9/4
C = racine(2 + 1/4) = racine(9/4) = racine(9)/racine(4) = 3/2 = 1,5
C est un nombre décimal, il appartient à l’ensemble D (et aussi aux ensembles Q et R)

Exercice 2 :

1)
2/3 - 1 = 2/3 - 3/3 = -1/3
2/15 - 1/20 = (2*20)/(15*20) - (1*15)/(20*15) = 40/300 - 15/300 = 25/300 = 1/12
A = (2/3 - 1)/( 2/15 - 1/20) = (-1/3)/(1/12) = (-1*12)/(3*1) = -12/3 = -4

2)
B+C = 2*racine(5) - 1 + 2*racine(5) + 1 = 2*racine(5) + 2*racine(5) = 4*racine(5)

B^2 = (2*racine(5) - 1)^2 = (2*racine(5))^2 - 2*2*racine(5)*1 + 1^2 = 4*5 - 4*racine(5) + 1 = 21 - 4*racine(5)

(2*racine(5) - 1)*(2*racine(5) + 1 = (2*racine(5))^2 - 1^2 = 4*5 - 1 = 19

3)
racine(98) = racine(49*2) = racine(49)*racine(2) = 7*racine(2)
2*racine(50) = 2*racine(25*2) = 2*racine(25)*racine(2) = 2*5*racine(2) = 10*racine(2)
racine(18) = racine(9*2) = racine(9)*racine(2) = 3*racine(2)
D = racine(98) - 2*racine(50) + racine(18) = 7*racine(2) - 10*racine(2) + 3*racine(2) = (7 - 10 + 3)*racine(2) = 0*racine(2) = 0

Exercice 3 :

1)
A = 3*(x + 2)^2 = 3*(x^2 + 2x*2 + 2^2) = 3*(x^2 + 4x + 4)

B = (3x - 6)^2 = (3x)^2 - 2*3x*6 + 6^2 = 9x^2 - 36x + 36 = 9*(x^2 - 4x + 4)

(2x - 3)*(2x + 3) = (2x)^2 - 3^2 = 4x^2 - 9
(2x + 3)*(x - 1) = 2x^2 + 3x - 2x - 3 = 2x^2 +x - 3
C = (2x - 3)*(2x + 3) - (2x + 3)*(x - 1) = 4x^2 - 9 - (2x^2 + x - 3) = 4x^2 - 9 - 2x^2 - x + 3 = 2x^2 - x - 6

2)
A = (x + 2)*(2x - 3) - 3*(2x - 3)*(3x + 1) = (2x - 3)*(x + 2 - 3*(3x + 1)) = (2x - 3)*(x + 2 - 9x - 3) = (2x - 3)*(-8x - 1)

B = x^2 - 25 = x^2 - 5^2 = (x + 5)*(x - 5)

C = 4*(x - 3)^2 - 49*(x + 2)^2 = 2^2*(x - 3)^2 - 7^2*(x + 2)^2 = (2*(x - 3))^2 - (7*(x + 2))^2 = (2*(x - 3) + 7*(x + 2))*(2*(x - 3) - 7*(x + 2)) = (2x - 6 + 7x + 14)*(2x - 6 - 7x - 14) = (9x + 8)*(-5x - 20) = (9x + 8)*(x + 4)*(-5)

Exercice 4 :

1)
On note B, l’aire de ABCD
ABCD est un carré donc sont aire est B = (3x - 5)^2
On note C, l’aire de AFED
AFED est un rectangle de longueur 3x - 5 et de largeur x + 2, donc son aire est (3x - 5)*(x + 2)
On note A, l’aire de BCEF
A = B - C = (3x - 5)^2 - (3x - 5)*(x + 2)

2)
(3x - 5)^2 = (3x)^2 - 2*3x*5 + 5^2 = 9x^2 -30x + 25
(3x - 5)*(x + 2) = 3x^2 - 5x + 6x - 10 = 3x^2 + x - 10
A = (3x - 5)^2 - (3x - 5)*(x + 2) = 9x^2 -30x + 25 - (3x^2 + x - 10) = 9x^2 -30x + 25 - 3x^2 - x + 10 = 6x^2 - 31x + 35

3)
A = (3x - 5)^2 - (3x - 5)*(x + 2) = (3x - 5)*(3x - 5) - (3x - 5)*(x + 2) = (3x - 5)*(3x - 5 - (x + 2)) = (3x - 5)*(3x - 5 - x - 2) = (3x - 5)*(2x - 7)

4)
Pour x = 5 on a
A = (3*5 - 5)*(2*5 - 7) = (15 - 5)*(10 - 7) = 10*3 = 30

Le 02 octobre 2022 à 17:07:11 :
tu peux faire un exo de physique chimie stp , j'suis en première
on revoit avec la prof les bases de la seconde, et récAp de tout les exos de 2nd...

Non désolé

Jakarta, erreur d'inattention, tu as écrit :
" (30*10^2)/(-8*10^-3) = 30/(-8*10) "
mais pour simplifier il faut multiplier par 10^-2 en haut et en bas, ce qui donne : 30/(-8*10^-5)=-375000
B=réel et entier relatif

d'ailleurs, tant qu'à faire voici ce que j'avais fait pour le 1 :

A)(racine(2)+2*racine(3))²
= (racine(2))²+2*racine(2)*2*racine(3)+(2*racine(3))²
=2+4*racine(6)+12
=14+4*racine(6) :
(Pour expliquer : 2*racine(2)*2*racine(3)= 2*2*racine(2)*racine(3)=4*racine(6) et ( 2*racine(3))² = 2²*(racine(3))² =4*3=12)
A= réel et irrationnel

B) le numérateur : 30*10^2
Le dénominateur : (-2*10^-1)^3 = (-0.2)^3 = -0.2*-0.2*-0.2=-0.008 = -8*10^-3
Donc : 30*10^2 / (-8*10^-3)
On multiplie par 10^-2 en haut et en bas, ce qui donne : 30/(-8*10^-5)=-375000
B=réel et entier relatif

C) racine(2)+(1/4) = racine(8/4)+(1/4) =racine(9/4)= racine9/racine4 = 3 /2
C=Réel, rationnel et décimal

Pour rappel :
entier naturel = 0, 1, 2…
entier relatif = …-2, -1, 0, 1, 2…
décimal : qui s’écrit avec un nombre fini après la virgule.
rationnel : les fractions
irrationnel : pi et les racines carrés, par exemple
réel : tous sont réels dans ton cas.
(un nombre iréel = i, le nombre imaginaire mais on voit ça en Terminale)

Pour le tableau :