Savoir & Culture

Suite à une discussion intéressante que j'ai eu avec un membre du forum sur la philosophie de l'esprit et mon désir de répondre sérieusement à la question de ce topic : https://m.jeuxvideo.com/forums/42-68-68393602-1-0-1-0-comment-repondre-a-ses-questions-existentielles.htm , j'ai essayé de former un tout des réflexions que j'ai pu construire, exposé en-dessous.
Je crée cependant un topic indépendant de la question initiale car j'estime que le message est trop long et aborde trop de choses par rapport à ce à quoi l'auteur voulait que son topic soit destiné.

------------------------------------------------------------------------------------------------------------------------------------------------------

Définitions brèves :

Ensemble : Collection d'entités définies et distinctes.

Totalité (ou Infinitude, ou Réalité) : Ce qui ne peut pas être fini par autre chose, qui n'existe par soi et que par soi et donc dont la seule propriété est son être. La Totalité est opposée à la modalité/la partie/la finitude, qui elle, peut être finie par autre chose et qui n'existe pas seulement par soi mais aussi par autre chose, ce à quoi elle est une modalité.

Épistémè : Ensemble des connaissances en tout genre et issues de toute faculté de l'esprit (conception du monde, sciences, philosophies…) propres à une conscience (pour ne pas répéter esprit).

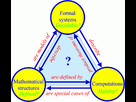
Système : Ensemble d'éléments considérés dans leurs relations à l'intérieur d'un tout fonctionnant de manière unitaire.

Langage : Ensemble de signes, de symboles ((formels ou informels) et de règles qui permettent d'assembler des énoncés.

Incomplétude : État de ce qui n'est pas complet, de ce qui n'est pas achevé. Plus concrètement, pour l'esprit humain, l'indécidabilité de certains énoncés implicites contenus dans un système (en tant qu'on les conçoit, il est possible d'y construire un langage par lequel il est possible de former ces énoncés).

Paradoxalité (d'un système) : Intrinsèquement liée à l'incomplétude, la paradoxalité correspond à l'état paradoxal partiel qu'un système contient. Plus concrètement, pour l'esprit humain, à la paradoxalité de certains énoncés implicites contenus dans un système (en tant qu'on le conçoit, il est possible d'y construire un langage par lequel il est possible de former ces énoncés paradoxaux)

Préfixe "Méta" (Wikipedia) : Méta est un préfixe qui provient du grec μετά (meta) (après, au-delà de, avec). Il exprime tout à la fois la réflexion, le changement, la succession, le fait d'aller au-delà, à côté de, entre ou avec.

Autoréférence : Propriété d'un énoncé dont le contenu sémantique est en relation avec cet énoncé, et qui, par cela même, est susceptible d'engendrer une antinomie.

------------------------------------------------------------------------------------------------------------------------------------------------------

Axiomes brefs :

I - L'axiome de la Totalité (la considération de la notion de Totalité d'une quelconque manière, explicitement ou implicitement) est indépassable par les facultés de l'esprit en tant qu'elles sont actuellement. C'est à dire qu'on ne peut considérer une activité des facultés de l'esprit (ou réflexion), sans faire appel d'une quelconque manière à cette présupposition.

II - En plus de l'obligation que pose l'axiome de la Totalité (par l'axiome I), les facultés de l'esprit humain sont contraintes, en tant qu'elles sont actuellement, quelque soit la réflexion qu'elles émanent, à toujours se "placer" épistémologiquement quelque part, c'est à dire à considérer des systèmes et les énoncés qu'on peut former à partir des langages qu'on peut construire à partir de ces mêmes systèmes (en tant qu'on les conçoit) comme plus "crédibles" ou plus précisément plus proches de la Totalité présupposée obligatoirement par l'axiome I, que d'autres énoncés issus d'autres systèmes (en tant qu'on les conçoit aussi) .

III - (Axiome d'extension des théorèmes d'incomplétude de Gödel : https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8mes_d%27incompl%C3%A9tude_de_G%C3%B6del )
- La présence d'axiome/présupposition/postulat/point de départ dans un système, en tant qu'il est conçu, augmente (ou du moins assure) l'incomplétude/paradoxalité partielle de ce dernier .

-------------------------------------------------------------------------------------------------------------------------------------------------------

Comment répondre à ces questions existentielles ?
(Question du topic à laquelle j'ai voulu répondre. Les termes sont un peu flous, mais le fond est plutôt clair. Je vais tenter d'y répondre par l'étude de la connaissance même, c'est à dire épistémologiquement.)

L'on peut penser plusieurs "réponses" à ces questions, même quand elles sont très bien posées.
Cela dit, certaines seront toujours considérées plus crédibles que d'autres selon chacun.

C'est à dire que, chez chaque personne, il y'a une idée profondément implicite et inextirpable de la Totalité (ou Réalité) en tant que Vérité Absolue et d'une hiérarchie "d'absoluité" (même si paradoxale) des systèmes (formels ou informels), c'est à dire de leur rapprochement (aux systèmes) à cette Totalité. (axiome I et II)

En effet, je pense qu'il nous est impossible de réfléchir sans supposer, même très implicitement, la notion de Totalité (axiome I), dont dérive le principe de non-contradiction dans une forme un peu plus imparfaite tel qu'il est formalisé. Ce n'est pas seulement le langage qui présuppose cela selon moi, mais carrément ce qui construit le langage, c'est à dire la cognition et/ou les facultés de l'esprit, d'une certaine manière.

On se place épistémologiquement (ce qui concerne toute forme de connaissance) toujours quelque part, de par notre finitude, ce qui nous pousse à considérer certains énoncés comme plus "crédibles" ou plus "vrais" que d'autres. (axiome II)

Même ceux qui refusent la Totalité comme concept, pensant s'en extirper, présupposent dans leur refus même la Totalité et une hiérarchie "d'absoluité", du fait qu'ils posent une impossibilité de conception de la Totalité qui est elle-même une tentative d'accéder à une conception de la Totalité en lui attribuant cette non-concevabilité, de plus qu'ils estiment qu'il est plus "crédible" et "raisonné" de faire cela (c'est à dire attribuer de par leur conception une propriété de non-concevabilité à la Totalité) que de considérer une possibilité (plus clairement une obligation) de conception de la Totalité, même bien imparfaite.

Autrement dit, ils établissent une relation d'hiérarchie de rapprochement avec leur conception de la Totalité en tant qu'elle possède la propriété de non-concevabilité, c'est à dire "d'absoluité" dans ce qu'ils ont conçu comme l'Absolu (ou la Totalité), hiérarchie entre le système qui associe la propriété de non-concevabilité et le système qui associe une obligation de conception de la Totalité, même imparfaite.

------------------------------------------------------------------------------------------------------------------------------------------------------

Néanmoins, cette idée même de hiérarchie "d'absoluité" peut mener à l'intérieur de nos systèmes, dans une tentative de description de cette idée, à des paradoxes (je montrerai plus bas pourquoi), c'est à dire que cette idée même est "paradoxale".

Certes elle l'est, mais c'est surtout qu'elle affirme implicitement dans son contenu qu'elle est incomplétude dans un système non-absolu et qu'une tentative de sa démonstration ou de son application dans un tel système va faire tendre à une structure paradoxale. Elle a une forme d'autoréférence (de même nature que celle du paradoxe de Russel (https://fr.wikipedia.org/wiki/Paradoxe_de_Russell), c'est à dire propre à l'universalité), dans laquelle elle dit que dans le langage où elle a été construite (ici issu d'un système fini), elle aura elle aussi une absoluité qui n'est pas infinie.

Description de la paradoxalité à laquelle on peut aboutir :

---

Si je veux décrire une hiérarchie/comparaison d'absoluité entre des systèmes, je suis obligé de le faire dans un système (en l'occurrence un méta-système), or l'absoluité de ce méta-système ne peut être non-comprise dans cette hiérarchie/comparaison d'absoluité pour parler de système de hiérarchie/comparaison d'absoluité, or pour inclure cela, il faut construire un méta-méta-système plus grand qui lui aussi doit avoir une absoluité et ainsi de suite...

On obtient ainsi une boucle récursive parce que l'on veut décrire l'Absolu dans le non-Absolu ou aussi parce que l'on veut appliquer une forme d'autoréférence universelle à une entité qui n'est pas en soi, mais aussi en autre chose (un système fini), c'est à dire qui ne se suffit pas réellement à elle-même.

---

Je pense que l'apparition de ces structures paradoxales de par l'autoréférence "universelle" est intrinsèquement liée au fait qu'on ne peut échapper épistémologiquement à l'axiome de la Totalité comme je l'ai énoncé dans l'axiome I couplé au fait que la présence d'axiome dans un système augmente (ou du moins assure) l'incomplétude/paradoxalité partielle de ce dernier (axiome III).

C'est pourquoi ces mécanismes tels que l'autoréférence menant à des structures paradoxales ne sont selon moi pas à ignorer, au contraire, car ils sont un signe de notre faiblesse épistémologique face à l'Absolu et donc possiblement d'un surpassement de cette dernière.

C'est donc selon moi ironiquement la paradoxalité à laquelle la considération d'une d'absoluité mène qui fait sa force, dans la considération d'une Totalité nous dépassant (en tant que facultés de l'esprit) et donc de notre finitude épistémologique fondamentale.

D'ailleurs, si la considération d'une absoluité pour un système ne menait pas à une structure paradoxale, elle mettrait à mal l'axiome III, car elle serait cohérente dans un système fini doté d'axiome/de postulat/de présupposition/de point de départ, alors qu'elle a prétention de saisir l'Absolu et d'user d'une autoréférence universelle.

C'est donc bien une généreuse chose, par rapport à ce que l'on a construit précédemment, que l'idée d'absoluité soit "paradoxale", ou mène à des structures paradoxales.

------------------------------------------------------------------------------------------------------------------------------------------------------

Finalement, cette hiérarchie "d'absoluité" qui s'impose comme une obligation à l'esprit laisse glisser la possibilité de progression de l'esprit comme un mouvement perpétuel de système en système. Cette possibilité ne correspond cependant qu'à une possibilité de progression, mais ne dit rien sur l'atteignabilité de la Totalité dans toute son infinitude.

Pragmatiquement, je ne pense pas que cette Totalité sera atteinte un jour par l'humanité, car, pour atteindre la Totalité qui est la même chose que la Réalité, la Réalité ne se démontrant totalement qu'elle même (par sa définition de ce qui n'existe qu'en soi et pas en autre chose ou autrement dit de son autosuffisance ontologique ; cela peut être aussi discuté plus rigoureusement par des formes de démonstrations malgré que pouvant êtres considérées comme imparfaites : https://m.jeuxvideo.com/forums/message/1137971614 (à lire avant si vous voulez comprendre le post linké précédemment, une tentative de définition rigoureuse et très formelle de la vérité : https://www.jeuxvideo.com.com/forums/message/1122166332 )), il faudrait tout simplement devenir la Réalité, où il ne fait plus trop de sens de toujours parler d'humanité en tant qu'elle est conçue dans l'Occident (les agents que sont les humains et leurs interactions internes correspondant à la société (assez différemment de la conception de l'humanité chez plusieurs Indiens par exemple, où cette dernière est considérée comme tout ce avec quoi l'homme interagit, d'une quelconque manière)).

Ainsi nous pouvons converger (comme faire le contraire) en tant que sujets en mouvement petit à petit vers la Totalité, vers le saisissement de l'essence de tout ce qui fait l'objet, en tant qu'il est chose infiniment complexe de la Réalité (ou plus simplement de toute sa réalité), telle une suite qui peut ne jamais parvenir à sa limite mais qui s'en approche toujours tant qu'elle avance (et seulement tant qu'elle avance, car si elle recule, c'est l'inverse qui se produit).

Réfléchir et accumuler du savoir, encore et encore... voilà une solution qu'on peut donner.

Penser atteindre un semblant de vérité objective dans un système (formel ou informel), puis faire face à l'incomplétude et la paradoxalité qu'il contient, puis dégager un nouveau système telle une unité dans la dualité que forme le système et son incomplétude/paradoxalité, puis répéter le processus indéfiniment.
Cela dit, ce même processus ne doit pas être employé n'importe comment pour penser avoir un semblant de progression, car il est très difficile de faire face à la paradoxalité et l'incomplétude, ne serait-ce que dans leur détection non-biaisée, mais aussi et surtout de dégager une unité (pertinente et indéformée par diverses lacunes logiques) de la dualité que forment un système et son incomplétude/paradoxalité.

------------------------------------------------------------------------------------------------------------------------------------------------------

Ta réflexion pourrait être intéressante, mais malheureusement, tu tombes dans le même écueil que beaucoup en continuant à raisonner à partir d'axiomes ; quand bien même tu invoques ici le théorème de Gödel pour essayer de contourner la question.

Votre gros soucis, c'est que vous êtes juste incapables de comprendre que ce n'est pas avec les mathématiques, et/ou la logique formelle que vous réussirez à résoudre les questions soulevées ici - du fait même que vous n'arrivez toujours pas à intégrer que ces formes d'entendement ne permettent de décrire que ce qui est à partir des axiomes posés devant soi ; mais pas comment cela est apparu, et vers quoi cela tend à évoluer.

Néanmoins, le fait que tu retiennes tout de même ici le principe de totalité dans ta réflexion, et comprennes que les relations n'ont de sens que par rapport au Tout dont elles dépendent permet de la sauver quelque peu. Et te place à un bien meilleur niveau que nombre d'idiots ici qui débarquent avec leurs platitudes relativistes inconsistantes.
Il ne te reste plus désormais qu'à découvrir la dialectique : et alors tu seras au top.

Votre gros soucis, c'est que vous êtes juste incapables de comprendre que ce n'est pas avec les mathématiques, et/ou la logique formelle que vous réussirez à résoudre les questions soulevées ici - du fait même que vous n'arrivez toujours pas à intégrer que ces formes d'entendement ne permettent de décrire que ce qui est à partir des axiomes posés devant soi ; mais pas comment cela est apparu, et vers quoi cela tend à évoluer.

Je veux bien mais comment est-ce possible d'émaner, pour les facultés de l'esprit, une activité de réflexion, sans avoir de point de départ épistémique, lié intrinsèquement à la finitude de ces mêmes facultés, c'est à dire ce qu'on appelle autrement un axiome ?

Pour moi, la logique formelle dont j'use dans mon raisonnement (qui s'approche d'avantage à de la métalogique - c'est à dire d'une logique traitant de la logique) est surtout une tentative de clarification et de perfection (dans le sens d'éviter les lacunes auxquelles le langage peut mener) du langage courant dont tant de philosophes font l'usage dans leurs textes. Néanmoins, dans le fond, je ne m'écarte pas de leur voie de pensée, c'est simplement la syntaxe qui change considérablement.

Bien que je n'ai toujours pas lu Hegel ou Kant, j'imagine qu'ils usent du langage courant (même si apparemment très recherché, ce qui rend bien plus complexe l'assimilation de la syntaxe du texte) et que de par leur finitude épistémique, leur expérience et leurs chemins de pensée, se trouvent confrontés, dans la construction de leur philosophie, à partir de quelque chose, c'est à dire présupposer/axiomatiser/être le point de départ de quelque chose par rapport à autre chose. Cela peut être même très implicite et imperceptible en apparence, mais dans le fond, je ne vois pas comment de notre finitude, nous pouvons nous extirper de cette obligation.

Selon moi et comme expliqué plus haut, la seule manière de ne pas avoir de point de départ pour un système et d'être complet, c'est simplement d'être la Totalité, tous ceux (les systèmes) voulant concourir à ce même système étant finis par rapport à ce dernier, donc devant au moins partir comme point de départ par rapport à lui, c'est à dire, de manière plus formalisée, à considérer un ou des axiomes.

Le 11 décembre 2021 à 13:10:

Ta réflexion pourrait être intéressante, mais malheureusement, tu tombes dans le même écueil que beaucoup en continuant à raisonner à partir d'axiomes ; quand bien même tu invoques ici le théorème de Gödel pour essayer de contourner la question.

et tu fais comment, pour raisonner sans axiomes ? Ton truc, c'est d'être abonné aux logiques de régression à l'infini ?

@ Arajinw J'ai pas encore fini de lire, mais il y a un truc qui me chiffonne, je te fais un retour dessus tout de suite :

à propos de la Totalité :

Ce qui ne peut pas être fini par autre chose, qui n'existe par soi et que par soi et donc dont la seule propriété est son être. La Totalité est opposée à la modalité/la partie/la finitude, qui elle, peut être finie par autre chose et qui n'existe pas seulement par soi mais aussi par autre chose, ce à quoi elle est une modalité.

d'après ce que je comprends c'est à la fois - une espèce de cosmos /Univers /ensemble de tout ce qui est (pas fini par autre chose)
- quelque chose qui existe par lui-même (Dieu au sens strict de ce qui n'a pas de cause, et n'a pas été créé, mais existe éternellement).

(comme la Nature selon Spinoza ?)

Est-ce que j'ai bon ?

(N.B.: sinon, pur la totalité, en continuant la lecture, ça me fait penser au Monde des Idées de Platon...)

à propos de la Totalité :

Ce qui ne peut pas être fini par autre chose, qui n'existe par soi et que par soi et donc dont la seule propriété est son être. La Totalité est opposée à la modalité/la partie/la finitude, qui elle, peut être finie par autre chose et qui n'existe pas seulement par soi mais aussi par autre chose, ce à quoi elle est une modalité.

d'après ce que je comprends c'est à la fois - une espèce de cosmos /Univers /ensemble de tout ce qui est (pas fini par autre chose)

- quelque chose qui existe par lui-même (Dieu au sens strict de ce qui n'a pas de cause, et n'a pas été créé, mais existe éternellement).

(comme la Nature selon Spinoza ?)

Est-ce que j'ai bon ?

Oui, ce qui est entendu par Totalité est très similaire à ce que Spinoza voulait entendre par Dieu, ce philosophe m'ayant pas mal inspiré dans mon parcours de manière générale.
Cela dit, Spinoza ajoute à son Dieu un peu plus de propriétés que la simple Totalité telle que je la décris, donc il est plus exact de parler de substance/cause en soi (même si pour Spinoza, cela est équivalent à Dieu comme il cherchera à le démontrer dans le livre I).

A la propriété d’être « cause de soi » un être qui se cause lui-même, qui existe entièrement par soi, entraine de soi seul sa propre existence (sans besoin d’une autre cause) ; causalité interne (auto-causalité) et non externe (hétéro-causalité), causalité absolue (indépendance causale) et non relative. Dans le concept de cause de soi « s’évanouit la distinction de la cause et de l’effet »

-

« être en soi » (ce que l’on peut appeler « inséité ») : se suffire complètement à soi-même, n’appartenir qu’à soi, être indépendant de toute autre chose ; un « absolu », une réalité absolument autonome (non relative, relative à rien d’extérieur).

Je veux bien mais comment est-ce possible d'émaner, pour les facultés de l'esprit, une activité de réflexion, sans avoir de point de départ épistémique, lié intrinsèquement à la finitude de ces mêmes facultés, c'est à dire ce qu'on appelle autrement un axiome ?

Justement, en essayant de recomposer le processus même qui a permis de poser ces axiomes. Je viens de te le dire.

Or, pour y parvenir, tu ne le peux pas via le positivisme - du fait même de son principe qui est bien celui de poser des hypothèses devant soi, et de démontrer tout ce qui découle d'elles, de façon déductive.
Je sais que c'est extrêmement dur à accepter pour un scientifique, mais c'est pourtant bien là la seule solution pour pouvoir remonter au delà des axiomes, vers le(s) sujet(s) de la connaissance et le(s) jugement(s) synthétique(s) a priori - pour reprendre ici une terminologie kantienne- à partir desquels la base axiomatique trouve son origine.

Il faut bien passer ici de la logique formelle à la logique dialectique : la seule qui soit en mesure de recomposer le processus de définition des axiomes avant même qu'ils n'aient été posés, et même définis. Sans ça, tu ne peux dire que ce qui est, et non comment cela est apparu, et vers quoi cela tend. Désolé de le répéter.

il faudrait tout simplement devenir la Réalité, où il ne fait plus trop de sens de toujours parler d'humanité en tant qu'elle est conçue dans l'Occident

Il n'y a pas à le devenir, tu l'es déjà, tu es toute la réalité et par là même, tu es toute la vérité antéprédicative. Et tu le "sais". Mais tu ne le sais pas par le langage (ni même par un langage phénomenal), mais tu le sais par ta phénoménologie. Effectivement, on ne doit pas parler d'humanité car il n'y a pas d'homme : "l'homme est le rêve d'une ombre" (Pindare). Il n'y a pas de cosmos, pas de monde ordonné, pas de logique, pas de substance, pas d'homme, pas de langage, mais seulement l'insubstantialité de l'apparence, l'instabilité, l'indifférence, et l'homogénéité pure.

Le 11 décembre 2021 à 17:31:33 :

Je veux bien mais comment est-ce possible d'émaner, pour les facultés de l'esprit, une activité de réflexion, sans avoir de point de départ épistémique, lié intrinsèquement à la finitude de ces mêmes facultés, c'est à dire ce qu'on appelle autrement un axiome ?

Justement, en essayant de recomposer le processus même qui a permis de poser ces axiomes. Je viens de te le dire.

Or, pour y parvenir, tu ne le peux pas via le positivisme - du fait même de son principe qui est bien celui de poser des hypothèses devant soi, et de démontrer tout ce qui découle d'elles, de façon déductive.
Je sais que c'est extrêmement dur à accepter pour un scientifique, mais c'est pourtant bien là la seule solution pour pouvoir remonter au delà des axiomes, vers le(s) sujet(s) de la connaissance et le(s) jugement(s) synthétique(s) a priori - pour reprendre ici une terminologie kantienne- à partir desquels la base axiomatique trouve son origine.

Il faut bien passer ici de la logique formelle à la logique dialectique : la seule qui soit en mesure de recomposer le processus de définition des axiomes avant même qu'ils n'aient été posés, et même définis. Sans ça, tu ne peux dire que ce qui est, et non comment cela est apparu, et vers quoi cela tend. Désolé de le répéter.

La recomposition du processus même n'a-t-elle pas elle même un point de départ épistémique implicite témoignant de sa finitude épistémique, n'étant toujours pas parvenue à la Totalité (malgré que pouvant s'en approcher, c'est à dire en s'extirpant petit à petit des axiomes, de sa finitude, de ce qu'elle est en tant que possédant un point de départ par rapport à autre chose) ?

La logique dialectique (que je constate maintenant être très proche voire équivalente à ce que j'ai voulu dégager dans mon dernier paragraphe) se recompose incessamment dans son mouvement par la remontée aux axiomes, certes, mais tant qu'elle n'est pas parvenue à la Totalité, ne peut-t-elle pas ne pas contenir un point de départ épistémique concordant avec sa finitude par rapport à la Totalité (n'ayant toujours pas atteint cette dernière) ?

La recomposition du processus même n'a-t-elle pas elle même un point de départ épistémique implicite témoignant de sa finitude épistémique, n'étant toujours pas parvenue à la Totalité (malgré que pouvant s'en approcher, c'est à dire en s'extirpant petit à petit des axiomes, de sa finitude, de ce qu'elle est en tant que possédant un point de départ par rapport à autre chose) ?

Ce que je vais te répondre va très probablement te sembler un peu énigmatique : mais ce qui pose la fin même d'un terme axiomatique, c'est lorsque dernier rencontre sa contradiction. Et pour qu'il y ait contradiction, il faut d'abord qu'il y ait déjà avant tout diction. Tu vas mieux comprendre avec ce qui suit.

La logique dialectique (que je constate maintenant être très proche voire équivalente à ce que j'ai voulu dégager dans mon dernier paragraphe) se recompose incessamment dans son mouvement par la remontée aux axiomes, certes, mais tant qu'elle n'est pas parvenue à la Totalité, ne peut-t-elle pas ne pas contenir un point de départ épistémique concordant avec sa finitude par rapport à la Totalité (n'ayant toujours pas atteint cette dernière) ?

Pour mieux comprendre la logique dialectique, je vais t'en résumer brièvement un aperçu telle qu'elle se présente par exemple chez Hegel :

La chose la plus large qu'il nous soit donné de penser en tant que ce sujet cherchant à connaitre la vérité ; c'est que, tout comme l'avait signalé à juste titre Parménide : "Tout ce qui est, est". Quoique l'on essaye de saisir comme objet pour notre connaissance, cette vérité demeure quoi qu'il arrive toujours vraie. Il suffit de s'arrêter même juste un instant sur cette vérité fondamentale, pour constater à quel point elle est totalement absolue : Tout ce qui est, est.
Ensuite, une fois qu'on en a bien fait tout le tour de cette vérité dans son absoluité, on ne peut en rester là nous dit Hegel : car lorsque nous avons parfaitement goûté à l'absoluité de l'Être dans sa totalité, vient irrémédiablement le moment de la contradiction, et du passage de l'Être dans celle ci, à savoir de l'Être dans le non-Être. Ici nous devons d'abord comprendre que jamais nous n'aurions su penser le non-Être, sans avoir d'abord pensé l'Être. Et que c'est d'abord puisque nous avons dit l'Être, qu'ensuite nous avons pu le contredire par son non-Être.
Mais là encore on ne peut en rester là, car aussitôt le non-Être lui aussi saisit (comme terme contradictoire à l'Être), lui aussi en vient immédiatement à être de nouveau contredit et à se contredire par le fait qu'à partir du moment où il a pu être saisit : il est également. Il n'est certes plus l'Être tel que nous l'avions appréhendé initialement, mais pourtant il est ; c'est à dire qu'il est un Être autre enrichi par sa contradiction dans le non-Être. Notre Être initial, saisit dans tout ce qu'il avait de plus absolu est passé dans son Être autre, et via sa contradiction il est devenu Autre dans son devenir. Ici nous venons sans nous apercevoir de saisir le second Concept qui nous permet de renvoyer dos à dos l'Être et sa contradiction le non-Être, grâce à son devenir. De manière à ce que nous soyons désormais en mesure de dire et de penser que Tout ce qui est devient.
C'est là un grand pas qui vient d'être franchi, mais on ne peut toujours pas en rester là. Car maintenant nous devons tout autant essayer de saisir toute les conséquences de ce que nous venons de définir comme toujours vrai dans ce que nous venons d'exposer : le devenir lui aussi certes est, mais contrairement à l'Être, il ne peut pas basculer dans le non-Être ou le non-devenir car nous en reviendrions au point de départ, et ne pourrions plus suivre l'Être dans sont déploiement dialectique tout en conservant tous les termes que nous avons su saisir jusqu'ici. La façon de s'en sortir ici est tout simplement de constater que nous sommes parti au départ d'un Être là, mais qu'en devenant Autre : un Ceci est devenu un Cela. Etc.

Bref, tu peux parfaitement voir ici comment grâce à la dialectique, nous réussissons à voir comment nous arrivons à définir les termes avant même qu'ils ne nous servent base axiomatique, et comment avant toute hypothèse, nous réussissons à les faire apparaitre dans leur déploiement dialectique en remontant vers le(s) sujet(s) de la connaissance.
Sinon, pour la suite : just go read Hegel.

Je viens de tomber par hasard sur ce topic et si j'ai bien compris l'interrogation principale est une justification et explication fondamentale du réel dans son ensemble. Une théorie du tout philosophique "https:///wiki/Théorie_du_tout_(philosophie".

D'après Nicholas Rescher une telle entreprise nécessite d'abandonner le principe de non-circularité puisqu'une théorie capable de tout expliquer devra également pouvoir s'expliquer elle-même, et c'est pour cette raison que je ne suis pas un fondationnaliste mais un cohérentiste (comme l'op si j'ai bien suivi).
Je tiens à préciser que je suis + un matheux qu'un philosophe mais les questions métaphysiques m'ont toujours fascinées.
Pour commencer il faut un langage dans lequel la théorie doit s'inscrire et le seul langage possible est le langage mathématiques, purement syntaxique, sans signification et bagage humain, donc objectif.

Ainsi se pose les questions : Pourquoi y a t-il quelque chose plutôt que rien? (Gottfried Wilhelm Leibniz)
D'où provient la déraisonnable efficacité des mathématiques en physique? (Eugène Wigner)
Qu'est-ce qui insuffle le feu aux équations et leur fournit un univers à décrire? (Stephen Hawking) ou même pourquoi le monde est compréhensible?

Mon hypothèse se base sur une vision réaliste du monde, plus particulièrement un réalisme structurel ontique, lequel postule que les seules entités réelles sont les objets et relations qu'ils entretiennent (un objet n'a aucune propriété en soi), cette position philosophique est supportée par la physique mathématiques contemporaine comme la théorie quantique des champs où l'électrodynamique quantique n'est que le groupe unitaire U(1), la théorie unifiée électrofaible U(2) et SU(3)/Z(3) pour l'intéraction forte, toutes ces théories sont des théories dites de jauges, en ce sens les objets fondamentaux sont ontologiquement secondaire aux structures puisque les objets d'une théorie sont des membres de classes d'équivalences sous certaines transformations (symétries) et aucune autre individuation des objets n'est possible, cette vision m'a conduit directement à m'interroger sur la discipline étudiant les relations objectives (dépourvues de tout bagage humain) entre les objets, les mathématiques.
Il en vient que la description appropriée de la réalité n'est autre que mathématiques, si seules les entités mathématiques existent, alors la réalité physique n'est autre que mathématiques, c'est l'hypothèse de l'univers mathématiques : https://en.wikipedia.org/wiki/Mathematical_universe_hypothesis https://arxiv.org/pdf/0704.0646.pdf

Définissons d'abord ce qu'est une structure mathématiques : Une structure mathématiques est un ensemble d'objets sans propriétés mais dont les relations qu'ils entretiennent permettent d'exhiber ses propriétés, formellement c'est un triplet (A,o,I) où A est un ensemble non vide, o la signature et I une interprétation qui indique comment la signature doit être interprété sur A (le domaine). Évidemment cette définition en théorie des modèles s'applique uniquement sur les théories mathématiques de la logique du premier ordre ce qui est en désaccord avec toutes nos théories physique actuelles.

On dit que 2 structures mathématiques sont isomorphes s'il existe une correspondance entre tous les objets des 2 structures, dans le cas général on parlera d'isomorphisme naturel en théorie des catégories.
Si notre réalité physique est isomorphe à une structure mathématique alors notre réalité physique est une structure mathématique, par définition de l'isomorphisme.
On peut ainsi énumérer les structures mathématiques, des plus simples aux plus complexes, dans une liste que l'on pourra coder, de sorte que le code soit minimal afin d'éviter toutes redondances inutiles, comme bon nous semble (100 = l'ensemble/le type vide "1 ensemble/type, 0 relation et 0 objet) , 107 = ensemble/type à 7 objets sans relations, on peut ainsi continuer et énumérer des structures de plus en plus complexe comme l'espace de Hilbert, la théorie quantique des champs, le groupe E8 etc...), à noter que les termes "ensembles ou types" n'ont rien de fondamentaux, ce sont les mêmes éléments exprimés dans 2 théories distinctes.
Toutes ces structures existent, ce sont des univers à part entière, bien que certaines soient excessivement simples, et d'autres monstrueusement complexes.

On sait depuis Gödel que les mathématiques sont fondamentalement incomplètes, il existe des propositions indécidables et des énoncés vrais mais indémontrables.
Ces problèmes viennent principalement du fait que nous considérons des éléments infinis, l'incomplétude et l'indécidabilité disparaissent quand on restreint nos structures mathématiques aux fonctions récursives (ou calculables).
Une fonction f est une fonction calculable s'il existe une méthode précise qui, étant donné un argument x, permet d'obtenir l'image f(x) en un nombre fini d'étapes.
Ainsi le corps des nombres réels n'a pas d'existence propre et définie car non calculable, de même que l'opérateur de dérivation ou le concept de limite.
Toutes nos théories physique actuelles sont non calculables, elles supposent que la réalité physique est un continuum, donc nécessitent une infinité de bits d'informations à sa description SpoilAfficherMasquerUn problème a été posé par Hermann Weyl sur l'inapplicabilité du théorème de Pythagore dans un espace discret https://en.wikipedia.org/g/wiki/Weyl%27s_tile_argument, cependant des solutions provenant de la géométrie finitiste résolvent le problème https://plato.stanford.edu/entries/geometry-finitism/#ProExaUsiGra
Certaines fonctions comme l'exponentielle, le sinus ou le logarithme ne sont pas calculable mais le théorème de Stone-Weierstrass (dont la preuve est constructive) nous dit que toutes fonctions continues sur un intervalle [a,b] peuvent être uniformément approchées par une fonction polynomiale, qui elle est calculable.
En ce sens l'hypothèse de l'univers calculable est à privilégier, pour ce faire il nous faut renoncer à une approche naïve classique des mathématiques, les mathématiques calculables (sans rentrer dans les détails) sont l'interprétation de réalisabilité des mathématiques constructives.
En ce qui concerne la complexité, il existe des sous-structures d'une structure globale plus complexes que la structure globale, ça vient principalement de la complexité de Kolmogorov.
Par exemple l'ensemble des entiers naturels est moins complexe que l'une de ses parties, disons un googolplex, dans le sens où un simple programme (i=1
while i<i+1;
print(i)
i+=1) nécessite moins de bits d'informations à sa description que le nombre googolplex, on peut ainsi programmer un algorithme nécessitant moins d'informations à sa description que la séquence de nombres choisis aléatoirement dans l'ensemble généré par l'algorithme, ici les entiers naturels, ainsi on doit spécifier l'algorithme et son emplacement dans la séquence que produit l'algorithme, sa description requiert ainsi + d'informations que la structure complète.
On peut enfin mesurer la quantité d'information de l'univers, du multivers 1,2, 3 ou 4 SpoilAfficherMasquerMultivers de niveau 1 : extension de l'univers observable, Multivers de niveau 2 : bulles d'univers inflationnaire, Multivers de niveau 3 : mondes multiples de la physique quantique et enfin du multivers mathématiques, celui de niveau 4.
Il se trouve que la quantité en information de la réalité selon cette hypothèse est précisément nulle.

En effet, tout ce qui est possible existe nécessairement, ainsi la complexité de Kolmogorov est nulle, il n'y a rien à spécifier, 0 paramètre libre.

Enfin il existe une relation particulière entre structures mathématiques, algorithmes et systèmes formels, ils pourraient n'être que différentes facettes de la même chose 

C'est l'objet de l'idée du computational trinitarianism : https://ncatlab.org/nlab/show/computational+trinitarianism 

On y voit un parallèle évident, cela pourrait représenter notre réalité.

On a considéré que seuls les objets abstraits dépourvu de tout bagage humain, donc de nature mathématiques, avaient une existence physique, ce que nous considérons comme physique est en fait purement relationnel (ou mathématiques), tout comme un univers simulé n'est rien d'autres que son programme (il y a d'ailleurs une correspondance entre preuves et programmes cf : isomorphisme de Curry-Howard).
Mais alors une question persiste, pourquoi les objets mathématiques existent? Pourquoi les lois de la logique existent?

Ici l'algèbre nous aide à y répondre, on peut formaliser la logique (classique, intuitionniste, etc.) comme des structures mathématiques indépendantes : https://en.wikipedia.org/wiki/Algebraic_logic

Mais dans ce cas pourquoi ces structures existent? Qu'est-ce qui justifient leur existence? C'est la question fondamentale auquel le fondationnalisme ne peut pas répondre, mais si on suppose qu'il y a un moyen de justifier les axiomes de ces structures dans les structures elles-mêmes alors la question n'aura plus de raison d'être puisque tout se justifiera tout seul, l'abandon du principe de non-circularité doit cependant être accepté.
Il est aussi à noter que l'ensemble de toutes les structures mathématiques ne forme pas une structure mathématiques, évitant ainsi les paradoxes à la Russell.

J'entends aussi des objection lié à la conscience : nos pensées ont un sens, ce n'est pas qu'un algorithme manipulant des symboles dans une structure neuronales complexes? Si le cerveau est une machine de Turing (computationnalisme) alors la sémantique (le sens) est un produit de la syntaxe. Chomsky a des travaux en linguistique sur le sujet.

À noter que Cristian S. Calude et Helmut Juergensen ont montré qu'un système raisonnable de preuves ne peut démontrer que des énoncés E dont la complexité d(E)=K(E)-longueur(E), où K est la complexité de Kolmogorov, est inférieure à une constante k (dépendant du système) auquel cas on se heurte à l'indécidabilité de Gödel.
L'informatique est vraiment intrinsèquement lié aux mathématiques.

Et pour les gens philosophes qui se sentent au dessus en croyant que la philosophie est nécessaire à l'existence même des mathématiques, la syntaxe des langages est donné par des monoïdes syntaxiques et leurs semantiques par une théorie des types, lesquelles sont purement intégrées dans le champs des mathématiques.

Sinon j'ai bien aimé ta rigueur et ta brève allusion à la théorie des modèles l'op.