geci
Salut à toi.
- Je pense que ta question tombe parfaitement dans le sujet que j'aborde dans ce topic : https://m.jeuxvideo.com/forums/42-68-68455807-1-0-1-0-reflexions-sur-l-etre-l-esprit-la-connaissance-et-la-totalite.htm
- En résumé je pense qu'il est toujours possible de créer une forme de paradoxe ou de boucle infinie avec un système formel, les axiomes qui lui servent de point de départ et son langage, ou du moins qu'une structure similaire à un paradoxe ou à une boucle infinie puisse y être contenue. Je prends pour simple exemple le paradoxe du menteur et son système formel de départ la logique propositionnelle/quantificationnelle qu'il est aisé de construire grâce un processus d'autoréférence.
Pour comprendre le passif de ce post, il est intéressant de lire ces posts :
- https://m.jeuxvideo.com/forums/message/1122166332
- https://m.jeuxvideo.com/forums/message/1137971614
Ce sont des tentatives de ma part de définir rigoureusement la vérité en conciliant les définitions de vérité-correspondance et de vérité-cohérence.
- Théorie de la vérité-correspondance : https://fr.wikipedia.org/wiki/Th%C3%A9orie_de_la_v%C3%A9rit%C3%A9-correspondance
Cette théorie s'oppose en particulier à la conception de la vérité en tant que cohérence, qui affirme que la vérité d'une proposition ne dépend pas de son rapport au monde, mais de ses relations avec d'autres propositions. Ces deux théories s'opposent donc sur la nature du rapport entre le langage et le monde. Les tenants d'une conception de la vérité en tant qu'adéquation avec le monde sont le plus souvent aussi tenants d'une conception réaliste, affirmant l'existence du réel indépendamment de nos perceptions. Toutefois, on peut soutenir une conception de la vérité en tant que correspondance tout en partageant une position idéaliste.
Le 16 août 2022 à 14:16:38 :
geci
Que dois-je comprendre ?
Salut à toi.
Je pense que ta question tombe parfaitement dans le sujet que j'aborde dans ce topic : https://m.jeuxvideo.com/forums/42-68-68455807-1-0-1-0-reflexions-sur-l-etre-l-esprit-la-connaissance-et-la-totalite.htm
En résumé je pense qu'il est toujours possible de créer une forme de paradoxe ou de boucle infinie avec un système formel, les axiomes qui lui servent de point de départ et son langage, ou du moins qu'une structure similaire à un paradoxe ou à une boucle infinie puisse y être contenue. Je prends pour simple exemple le paradoxe du menteur et son système formel de départ la logique propositionnelle/quantificationnelle qu'il est aisé de construire grâce un processus d'autoréférence.
Pour comprendre le passif de ce post, il est intéressant de lire ces posts :
https://www.jeuxvideo.com.com/forums/message/1122166332
https://www.jeuxvideo.com.com/forums/message/1137971614
Ce sont des tentatives de ma part de définir rigoureusement la vérité en conciliant les définitions de vérité-correspondance et de vérité-cohérence.
Théorie de la vérité-correspondance : https://fr.wikipedia.org/wiki/Th%C3%A9orie_de_la_v%C3%A9rit%C3%A9-correspondance
Cette théorie s'oppose en particulier à la conception de la vérité en tant que cohérence, qui affirme que la vérité d'une proposition ne dépend pas de son rapport au monde, mais de ses relations avec d'autres propositions. Ces deux théories s'opposent donc sur la nature du rapport entre le langage et le monde. Les tenants d'une conception de la vérité en tant qu'adéquation avec le monde sont le plus souvent aussi tenants d'une conception réaliste, affirmant l'existence du réel indépendamment de nos perceptions. Toutefois, on peut soutenir une conception de la vérité en tant que correspondance tout en partageant une position idéaliste.
Intéressant, je vais lire ![]()
Est-ce que tu y traites de la manière dont on pourrait "modifier" ou "diminuer" cette part de paradoxe en toute logique ?
Intéressant, je vais lire
Est-ce que tu y traites de la manière dont on pourrait "modifier" ou "diminuer" cette part de paradoxe en toute logique ?
Après avoir mis en place l'idée que tout système formel ou informel possède en lui une part intriquée d'incomplétude et de paradoxalité, j'ai effectivement essayé de traiter de la manière dont pourrait se mobiliser cette incomplétude/paradoxalité selon le changement même de ce système.
Je l'ai d'abord fait dans le topic que je t'ai linké au tout début, mais agacé par la sorte de suffisance qu'émanait ma solution rapide à un problème si important, j'ai été confronté à devoir former un nouveau concept, qui pourrait dépasser cette difficulté. Je l'ai nommé "Onde" et il est en fait selon moi assez comparable au conatus de Spinoza ou à la dialectique chez Hegel (même si je n'ai pas lu Hegel).
Description brouillon du concept (Voir uniquement le texte dans les spoils en "Partie 1" et "Partie 2") ![]()
https://m.jeuxvideo.com/forums/message/1159367302
https://m.jeuxvideo.com/forums/message/1159367726
Ce topic (et d'autres mais surtout lui) m'a aidé à sa construction : https://m.jeuxvideo.com/forums/42-68-68856438-1-0-1-0-la-substance-un-concept-desuet.htm
J'ai lu une bonne partie des posts que tu as mis, je n'ai pas tout compris mais j'ai tout de même des remarques à poser. Prétends-tu que le système final (celui avec l'onde) auquel tu aboutis a figure de vérité absolue (ou pour être plus clair de ce que tu nommes toi-même système absolu) ? Est-ce que l'onde ne possède aucune incomplétude, aucun paradoxe, aucune relativité ? Dans ce cas, tu serais en fait auto-contradictoire. Je vais m'expliquer. Dans ton système même (qu'il soit plutôt formel ou plutôt informel), tu poses que tout système se déroulant en la connaissance de l'homme doit nécessairement être intriqué à une part de paradoxe. Tu poses en quelque sorte la nécessité de la relativité des systèmes de connaissances. Or l'onde, au final, n'est rien d'autre qu'un concept qui à émané du déroulement de ta connaissance, qui ne peut donc qu'être l'objet d'un système lié à une relativité et à une part de paradoxe. Prétendre donc que le système de l'onde a figure d'absolu te rendrait contradictoire. Pourtant, prétendre que l'onde a figure de relativité ne la ferait justement pas viser une forme d'absolu (alors que c'est ce qu'elle a l'air de vouloir faire, notamment en écrivant "Onde"), à moins que cet absolu soit relatif ? Comment comptes-tu articuler les rapports de l'absolu et du relatif dans ton concept d'onde pour faire face à ce paradoxe ?
C'est un point extrêmement pertinent et crucial que tu vises ici pour saisir ce que je veux entendre par l'Onde ; tu me rappelles d'ailleurs étrangement quelqu'un. 
L'Onde ne prétend pas à aboutir à une figure de vérité absolue. L'Onde est la description même de l'articulation entre les notions d'Absolu et de Relatif dans l'épistème. C'est l'idée même que dans un système de connaissances quelconque, l'on ne peut considérer l'un sans ignorer l'autre, car ils sont justement intriqués dans le cycle qui les décrit, qui est l'Onde. Quand je vise un relatif quelconque, je lui associe implicitement un absolu pour lequel il pourrait être relatif (souvent son support). Quand je vise un absolu quelconque, je lui associe implicitement un relatif pour lequel il pourrait justement être absolu (souvent ce qu'il "contient" en tant que support).
Comme je l'explique dans ma description de l'Onde, dans un cycle, un sens n'a pas à primer sur l'autre. L'on peut bien par exemple parcourir un cercle dans le sens horaire ou anti-horaire, au bout du compte, exactement les mêmes points du cercle ont été parcourus.
Ainsi l'Onde devient la tentative de description du cycle par lequel se font les mouvements allant pour un sens de l'Absolu au Relatif et pour l'autre du Relatif à l'Absolu, de manière complètement intriquée.
On peut m'objecter que cette tentative même de description du cycle de l'Absolu/Relatif, est soumise internement aux mouvements de ce cycle ; qu'ainsi nous pouvons aboutir à une régression à l'infini qui constitue une incomplétude. La chose étant que l'Onde s'englobe méta-récursivement, c'est à dire que dans la description même de son concept par les trois mouvements, toute application entre eux et quel qu'est leur nombre correspond à une manifestation de ce que décrit le concept de l'Onde.
En réalité, le troisième moment peut autant être considéré comme premier moment que le premier ou que le deuxième moments. Pareillement pour le deuxième moment. 1 -> 2 -> 3 ; 1 -> 3 -> 2 ; 2 -> 1 -> 3 ; 2 -> 3 -> 1 ; 3 -> 1 -> 2 ; 3 -> 2 -> 1 ; tous sont possibles.
Car logiquement, pour avoir pu poser mes trois moments, j'ai dû les penser dans un support qui permet la multiplicité, la différence et la richesse (que l'on nomme plus simplement l'espace-temps).
Aussi, pour penser mon troisième et deuxième moment, j'ai dû penser implicitement mon premier moment, car j'ai dû tout simplement penser.
Le troisième moment n'est troisième moment que dans un souci de formalisme épistémologique.
Les trois moments sont intriqués cycliquement (c'est à dire que non seulement ils sont intriqués, mais ils le sont carrément avec les applications sur eux-mêmes). Non seulement tous les sens 1 -> 2 -> 3 etc... sont possibles, mais aussi 1(1 -> 2 ->3), ou 1(1) ou 1(2) ou 1(3) ou 1(2->3) ou 1(3->2) ou ou 1(1 (->2)) ou 1(1(1(1)...)) ou 3(1(1(1))) ou 2(1->3(2(3(1(2->1))))ou 2(2(1(1->3))) etc...
Cela forme un cycle de dimensionnalité "infinie". On ne peut ainsi prétendre échapper de ce cycle quand on parle de ce que le cycle inclut lui-même, parce que ce dernier s'englobe méta-récursivement (c'est à dire qu'il englobe toute tentative de le saisir (par les trois moments qui le constituent) et ce récursivement (comme montré plus haut)). Le cycle ne dit pas qu'on ne peut pas le compléter, mais il dit qu'on doit le compléter (c'est à dire ne pas le fuir, l'ignorer, le détruire ; mais bien s'en servir pour le compléter).
Toute N-Méta-Onde est donc Onde
L'Onde contient en elle l'ensemble E(N-Méta-Ondes).
Par Méta-Onde, j'entends l'Onde (en un de ses trois moments) appliquée à l'Onde (en un de ses trois moments).
Par N-Méta-Onde, j'entends l'étape Nième, N un entier naturel, de l'appel à la fonction "Méta", c'est à dire l'appel de la fonction "Méta" à la Nième étape en la N-1-Méta-Onde.
Par exemple : 3-Méta-Onde = Méta(Méta(Méta(Onde)))). Littérairement ça donne : L'Onde appliquée à l'Onde appliquée à l'Onde appliquant l'Onde.
Par E(N-Méta-Onde), j'entends l'ensembles des N étapes, avec N un entier tendant vers +l'infini, des appels de la fonction "Méta" à la Nième étape en la (N - 1)-Méta-Onde.
Ce type de régressions à l'infini ne constituent donc pas un problème pour l'Onde, car c'est justement en partie sa méta-récursivité, donnant une solution au problème potentiel que pourrait poser la régression à l'infini, qui la caractérise.
Que donc la tentative même de décrire le cycle par lequel se font les mouvements allant pour un sens de l'Absolu au Relatif et pour l'autre du Relatif à Absolu de manière intriquée, soit elle même soumise internement aux articulations de ce cycle, ne constitue pas un problème.
L'Onde peut donc être absolue en tant que je lui attache implicitement une relativité dans le cycle mais aussi relative en tant que je lui attache implicitement une absoluité dans le cycle, mais elle est aussi cette double-articulation intriquée entre l'Absolu et le Relatif qui caractérise le cycle.
En résumé je pense qu'il est toujours possible de créer une forme de paradoxe ou de boucle infinie avec un système formel, les axiomes qui lui servent de point de départ et son langage, ou du moins qu'une structure similaire à un paradoxe ou à une boucle infinie puisse y être contenue. Je prends pour simple exemple le paradoxe du menteur et son système formel de départ la logique propositionnelle/quantificationnelle qu'il est aisé de construire grâce un processus d'autoréférence.
Ce que j'observe souvent en logique, c'est que les gens construisent des systèmes formels soit disant fondamentalement différents mais en fait ils utilisent le même formalisme pour les construire et c'est là où le bât blesse. Le problème est déjà dans leur façon initiale d'envisager la logique et de poser les problèmes. On ne peut pas décrire un bon système logique avec un mauvais langage et on ne peut pas avoir un bon langage avec un mauvais système logique.
Le système psycho-logique qui permettrait d'échapper aux paradoxes est vraisemblablement indescriptible depuis votre système psycho-logique. Il faudrait donc posséder ce système psycho-logique de manière innée, comme moi, mais je ne peux pas vous le communiquer par conséquent, ce n'est pas faute d'avoir essayé.
J'entends.
Donc ta quête est de trouver un terme au conflit philosophique entre les "absolutistes" (au sens d'affirmant la possibilité et même la réalisation d'une vérité absolue niée de toute relativité dans un système de connaissance) et les relativistes (considérant une irréductible part de relativité en tout système de connaissance) par ton concept d'onde, en synthétisant leurs idées dans une sorte de structure qui rend les deux positions plus ou moins compatibles internement à elle, qui peut être vue comme un cycle.
Si je comprends bien, tu définis l'onde comme l'ensemble des trois moments et la manière dont ils s'articulent. De cette définition, tu en déduis que l'onde représente aussi "le cycle par lequel se font les mouvements allant pour un sens de l'Absolu au Relatif et pour l'autre du Relatif à l'Absolu, de manière complètement intriquée" au sein de la connaissance.
Ton concept a un potentiel très intéressant. Je te conseille de décrire tes trois moments et leur connexion de manière plus rigoureuse mais aussi accessible pour le consolider et l'ouvrir à un public plus large, en traitant en profondeur les concepts qui y sont sous-jacents comme la dualité de la relation sujet-objet, l'unité présupposée de la dualité comme totalité de cette dualité ou "chose en soi", la multiplicité-différence-richesse etc...
(Le message est destiné à Arajinw au cas où)
Je suis impressionné de la rapidité avec laquelle tu m'as saisi ; c'est exactement ça.
Je prends compte de tes conseils et je les sais pertinents car c'est bien dans la manière dont se construisent et s'articulent les trois moments que se joue d'une part la méta-récursivité de l'Onde et d'autre part son équivalence au cycle de l'Absolu/Relatif, qui sont cruciales.
L'autre conseil que je me donne est de "concrétiser" mon concept en évitant de trop le traiter internement à l'entendement et à la raison seulement, c'est à dire en l'appuyant par l'expérience et en le facilitant pour la sensibilité (en le "matérialisant"). C'est la construction de l'onde qui part de l'être au connaitre (tandis que je me suis plutôt concentré sur la construction de l'onde qui va du connaitre à l'être).
Il n'y a rien de mieux qu'une étude approfondie de diverses sciences empiriques, formelles et humaines afin de parvenir à un tel but ou de comprendre son impossibilité, dont les neurosciences, les sciences cognitives, la biologie, la physique, la logique, les mathématiques, l'informatique, l'anthropologie, l'histoire, la psychologie etc...
C'est la démonstration de Gödel : un système logique est soit cohérent soit complet, pas les deux. C'est le théorème d'incomplétude.
Le 24 août 2022 à 19:22:33 :
C'est la démonstration de Gödel : un système logique est soit cohérent soit complet, pas les deux. C'est le théorème d'incomplétude.
- Les deux théorèmes d'incomplétude de Gödel n'ont pas encore été démontrés pour tout système formel cohérent mais ils ont en effet une très grande pertinence dans le cadre de ce sujet. C'est d'ailleurs pour cela que j'ai fait ce trick dans ce topic par le troisième axiome : https://m.jeuxvideo.com/forums/42-68-68455807-1-0-1-0-reflexions-sur-l-etre-l-esprit-la-connaissance-et-la-totalite.htm
III - (Axiome d'extension des théorèmes d'incomplétude de Gödel : https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8mes_d%27incompl%C3%A9tude_de_G%C3%B6del )
- La présence d'axiome/présupposition/postulat/point de départ dans un système, en tant qu'il est conçu, augmente (ou du moins assure) l'incomplétude/paradoxalité partielle de ce dernier .
- Les théorèmes de Gödel ont en effet encore des conditions d'applications qui ne leur permettent pas de s'étendre à tout système formel cohérent.
Le premier théorème d'incomplétude peut être énoncé de la façon encore un peu approximative suivante (les termes techniques sont expliqués dans le paragraphe suivant).
Dans n'importe quelle théorie récursivement axiomatisable, cohérente et capable de « formaliser l'arithmétique », on peut construire un énoncé arithmétique qui ne peut être ni démontré ni réfuté dans cette théorie.
De tels énoncés sont dits indécidables dans cette théorie. On dit également indépendants de la théorie.
Toujours dans l'article de 1931, Gödel en déduit le second théorème d'incomplétude :
Si T est une théorie cohérente qui satisfait des hypothèses analogues, la cohérence de T, qui peut s'exprimer dans la théorie T, n'est pas démontrable dans T.
Ces deux théorèmes sont valides par exemple pour l'arithmétique de Peano et donc pour les théories plus fortes que celle-ci, en particulier les théories destinées à fonder les mathématiques, telles que la théorie des ensembles ou les Principia Mathematica.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------
Les conditions d'application des théorèmes :
Pour fixer les idées, on considère dorénavant que les théories en question sont, comme celles que l'on vient de mentionner (arithmétique de Peano, théorie des ensembles), des théories du premier ordre de la logique classique, même si les théorèmes d'incomplétude restent valides, sous les mêmes conditions, par exemple en logique intuitionniste ou en passant à l'ordre supérieur.
Par théorie récursivement axiomatisable, on entend que la théorie peut être axiomatisée de façon qu'il soit possible de reconnaître purement mécaniquement les axiomes parmi les énoncés du langage de la théorie. C'est le cas des théories utilisées pour formaliser tout ou partie des mathématiques usuelles.
Une théorie est cohérente s'il existe des énoncés qui ne sont pas conséquence de ses axiomes ; ou autrement dit si elle ne démontre pas tous les énoncés. Une théorie incohérente permet de tout démontrer et est donc vide de sens. La cohérence est souvent exprimée sous la forme équivalente : aucune contradiction ne peut être prouvée à partir des axiomes. On dit aussi qu'elle est consistante ou non contradictoire. Pour pouvoir démontrer son premier théorème d'incomplétude sous sa forme la plus générale (il existe un énoncé qui n'est ni démontrable, ni réfutable dans la théorie) Gödel faisait une hypothèse de cohérence un peu plus forte. Cette hypothèse n'est toutefois pas nécessaire pour le second théorème, qui n'énonce que la non-démontrabilité de l'énoncé de cohérence. De plus, John Barkley Rosser a donné en 1936 une démonstration du premier théorème d'incomplétude sous cette simple hypothèse de cohérence. À proprement parler, l'énoncé du premier théorème d'incomplétude donné ci-dessus n'est donc pas exactement celui de Gödel ; pour cette raison on nomme celui-ci théorème de Gödel-Rosser.
Une théorie permet de formaliser l'arithmétique si, d'une part il est possible de définir (en un sens qu'il faudrait préciser) les entiers (donnés par zéro et la fonction successeur), avec les opérations usuelles, au moins l'addition et la multiplication, et si d'autre part un certain nombre d'énoncés sur les entiers sont prouvables dans la théorie. L'arithmétique de Peano est une telle théorie, et satisfait les hypothèses des deux théorèmes d'incomplétude. En fait une théorie arithmétique beaucoup plus faible suffit pour le premier (la récurrence n'est essentiellement pas utile). Pour le second, les preuves usuelles utilisent un minimum de récurrence.
Il est remarquable que pour formaliser l'arithmétique, l'addition et la multiplication suffisent (en plus de zéro et du successeur). C'est le tout premier pas vers la solution du dixième problème de Hilbert (voir théorème de Matiyasevich). L'addition seule ne suffit pas : l'arithmétique de Presburger, qui est la théorie obtenue en restreignant l'arithmétique de Peano au langage de l'addition (en plus de zéro et du successeur), est complète.
C'est bon tu vas y arriver ?
Le 25 août 2022 à 02:06:21 :
C'est bon tu vas y arriver ?
Chut, je veux avoir un affichage parfait.
@Arajinw
Bravo, tu fais du beau boulot, avec érudition, rigueur et réflexion.
J'aime beaucoup ta petite référence visuelle au nombre d'or et au diagramme dans ce lien :
https://m.jeuxvideo.com/forums/42-68-68455807-1-0-1-0-reflexions-sur-l-etre-l-esprit-la-connaissance-et-la-totalite.htm
Tu discutes bien ton axiome de "Totalité" et tu identifie bien que c'est un os, un gros caillou dans la botte.
Je suis totalement incapable de ta rigueur, je me suis pas suffisamment entrainé à ça. Mais rien n'empêche de prendre du plaisir pour autant, ça ruine juste définitivement toute prétention.
Depuis quelques mois je reprend cette question qui me cuit le cul et dont tu dis qu'elle permet de formaliser une arithmétique : c'est quoi un entier ?
Je peux pas en parler sérieusement pour le moment parce que je suis au point de chercher a formaliser des intuitions est c'est un gros bordel caca. Je cherche a dépayser le problème. Je réfléchis à partir de cette analogie que le vide et les échanges boursier on ceci en commun qu'ils sont des jeux à somme nulle. Je m'efforce de donner un sens, une représentation, a ce que serait une relation antérieur à l'objet. C'est paradoxale. L'horizon jubilatoire là dedant, c'est pas que je pense pouvoir trouver quelque chose de satisfaisant. Mais je pense que j'arriverai sur ce chemin a mieux comprendre la fonction zêta de Riemann.
Ca va m'occuper un certain temps, c'est en soi le principal intérêt sur le plan personnel ![]()
Les paradoxes n'existent pas, pour la simple et bonne raison que ils ne peuvent exister dans le réel par définition. Pour résumer, les paradoxes ne naissent pas d'un problème naturel(puisque l'impossibilité ne peut exister) mais d'un langage mal utilisé ![]()
Bravo, tu fais du beau boulot, avec érudition, rigueur et réflexion.
Merci. Tu me fais trop d'honneur. 
N'hésite pas à lire si ça t'as intéressé les autres posts que j'ai linké plus haut et ma conversation avec Larkamboise.
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------
J'aime beaucoup ta petite référence visuelle au nombre d'or et au diagramme dans ce lien
J'en suis ravi. Elles avaient pour but de transmettre l'idée que le mouvement de convergence des systèmes de connaissances du sujet à travers l'Espace-temps vers la Totalité ne se fait pas de manière plate et linéaire , mais bien plutôt sous un schéma (détails mathématiques en spoiler) :
I ○ Hélicoïdal 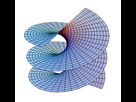
Un hélicoïde, ayant généralement le paramétrage suivant en coordonnées cartésiennes :
u ∈ ℝ , v ∈ ℝ, c ∈ ℝ, ∝ = c :
- x = v*cos(∝*u)
- y = v*sin(∝*u)
- z = u
Cette structure a été décrite par Euler en 1774 et par Jean-Baptiste Marie Meusnier en 1776. Son nom provient de sa similitude avec l'hélice : pour chaque point de l'hélicoïde, il existe une hélice contenue dans l'hélicoïde qui passe par ce point.
Plus d'informations :
- https://en.wikipedia.org/wiki/Helicoid
- https://en.wikipedia.org/wiki/Generalized_helicoid
II ○ Sphérique, cyclique 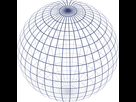
<spoil>Une 2-sphère
Pour un espace euclidien E (Un espace euclidien est un objet algébrique permettant de généraliser de façon naturelle la géométrie traditionnelle développée par Euclide, dans ses Éléments (plus d'infos ici : https://fr.wikipedia.org/wiki/Espace_euclidien ).) de dimension n+1, un point P de E et r un réel strictement positif (r ∈ ℝ+*) ; on nomme n-sphère (n ∈ ℕ) ou hypersphère de centre P et de rayon r l'ensemble des points M dont la distance à P vaut r.
Il est possible de se ramener à une n-sphère ou hypersphère centrée à l'origine étant donné un repère affine orthonormé par l'équation :
- ∑ (1 ≤ i ≤ n+1) xi² = r²
Par exemple :
- pour le cas n = 0, la 0-sphère est constituée de deux points d'abscisses respectives r et -r ;
- pour le cas n = 1, la 1-sphère est un cercle ;
- pour le cas n = 2, la 2-sphère est une sphère au sens usuel.
Plus d'informations :
- https://fr.wikipedia.org/wiki/N-sph%C3%A8re
- https://fr.wikipedia.org/wiki/Coordonn%C3%A9es_sph%C3%A9riques#G%C3%A9n%C3%A9ralisation
</spoil>
III ○ Transfigurant 
<spoil>Un attracteur de Lorenz sous les paramètres σ = 10, ρ = 28 et β = 8/3. Il est lié à la théorie du chaos en ce que le modèle de Lorenz censé décrire des phénomènes météorologiques en se basant sur la mécanique des fluides est un système dynamique tridimensionnel qui engendre un comportement chaotique dans plusieurs conditions.
Le système dynamique différentiel de Lorenz s'écrit :
I -
dx
---- = σ*[y(t) - x(t)]
dt
II -
dy
---- = ρ*x(t) - y(t) - x(t)*z(t)
dt
III -
dz
---- = x(t)*y(t) - β*z(t)
dt
où σ, ρ et β sont trois réels paramétrées strictement positifs (∈ ℝ+*), fixés. σ est le nombre de Prandtl ( https://fr.wikipedia.org/wiki/Nombre_de_Prandtl ) , et ρ abusivement dénommé « nombre de Rayleigh », est en fait le rapport du nombre de Rayleigh ( https://fr.wikipedia.org/wiki/Nombre_de_Rayleigh ) Ra au nombre de Rayleigh critique Rac (Rac est la valeur de Ra au-dessus de laquelle le système physique ne peut pas rester invariant au cours du temps, où donc il est sujet à des mouvements de convection).
Les variables dynamiques x, y et z représentent l'état du système à chaque instant. L'interprétation physique en est la suivante : x(t) est proportionnel à l'intensité du mouvement de convection, y(t) est proportionnel à la différence de température entre les courants ascendants et descendants, et z(t) est proportionnel à l'écart du profil de température vertical par rapport à un profil linéaire.
On pose souvent σ = 10 et β = 8/3, ρ restant variable. Le système présente un comportement chaotique pour ρ = 28, après un certain temps en régime pseudopériodique (de l'ordre de 30 secondes). Cette durée dépend de ρ : elle peut monter à 180 secondes pour ρ = 24,3.
L'attracteur de Lorenz est défini comme l'ensemble des trajectoires à long terme du système dynamique de Lorenz ci-dessus.
Lorsque les paramètres σ, ρ et β prennent les valeurs suivantes : σ = 10, ρ = 28 et β = 8/3, le système dynamique différentiel de Lorenz présente un attracteur étrange en forme d'ailes de papillon, représenté par l'image plus haut.
Pour presque toutes les conditions initiales (différentes de celles des points fixes), l'orbite du système s'approche rapidement de l'attracteur, la trajectoire commençant par s'enrouler sur une aile, puis sautant d'une aile à l'autre pour commencer à s'enrouler sur l'autre aile, et ainsi de suite, de façon apparemment erratique (instable).
Animation de l'attracteur de Lorenz pour ρ allant de 0 à 28 : https://upload.wikimedia.org/wikipedia/commons/d/d3/Lorenz_apparition_small.gif
Plus d'informations :
- https://fr.wikipedia.org/wiki/Attracteur_de_Lorenz
- https://fr.wikipedia.org/org/wiki/Th%C3%A9orie_du_chaos
</spoil>
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------
I ○ Ce mouvement se fait premièrement sous un aspect hélicoïdal parce qu'il se différentie fondamentalement d'une progression linéaire, droite et sans creux (donc plate). Il est globalement ascendant mais sous formes de va-et-vient, de croissances et de décroissances rotatives, de jaillissements et de refluements. C'est un flux continu qui s'étend à l'infini en aspirant à explorer les différents angles, aspects et perspectives et en les connectant à une structure continualisante en perpétuelle effervescence, en perpétuel moment. En tout point de l'hélicoïde, il existe une hélice contenue dans l'hélicoïde qui passe par ce point. En tout point du mouvement des systèmes de connaissance du sujet à travers l'Espace-temps vers la Totalité, il existe un système de connaissance, un paradigme, un angle, un potentiel, une relativité, qui passe par ce point. Ainsi se manifeste la méta-récursivité de ce mouvement, c'est-à-dire le fait que toute méta-application de ce mouvement sur lui-même et quelle qu'est sa dimensionalité, est décrite par le mouvement même.
Plus d'informations sur la méta-récursivité dans ce post issu de ma discussion avec Larkamboise plus haut :
- https://m.jeuxvideo.com/forums/message/1181940102
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------
II ○ Ce mouvement se fait deuxièmement sous un aspect sphérique/cyclique car il synthétise les pensées, intuitions, notions et concepts relativement duaux mis en jeu dans les systèmes de connaissance du sujet se déployant dans l'Espace-temps de manière à ce qu'ils soient intriqués en une même unité cyclique ; ce en explorant perpétuellement de nouvelles dimensionnalités.
Cela peut avoir pour origine l'unité même qui est présupposée dans toute pensée, pensée qui ne peut qu'être relation sujet-objet ; unité donc comme totalité de la dualité qu'est la relation sujet-objet, comme support ayant permis une telle relation. De l'impossibilité d'une part de saisir cette totalité unitaire présupposée en toute pensée duelle de manière fixe, immuable et absolue et d'autre part de l'imputation à ce support/totalité même les trois propriétés de donner successivement aux systèmes de connaissances duaux qu'il contient :
- Multiplicité
 il existe plus d'une relation sujet-objet et par extension plus d'un système de connaissance au sein du support qui les permet
il existe plus d'une relation sujet-objet et par extension plus d'un système de connaissance au sein du support qui les permet
- Différence
 les multiples systèmes en question ne sont pas identiques et peuvent se différencier de par au moins un élément
les multiples systèmes en question ne sont pas identiques et peuvent se différencier de par au moins un élément
- Valorisation
 les multiples systèmes qui se différencient de par au moins un élément ne peuvent avoir de valeur par rapport à la totalité unitaire/support (ayant figure d'absoluité) qui les permet mais bien par rapport à un agglomérat de systèmes (qu’on peut nommer super-système) internes à cette totalité des totalités, par lesquels se forme un système de valeurs
les multiples systèmes qui se différencient de par au moins un élément ne peuvent avoir de valeur par rapport à la totalité unitaire/support (ayant figure d'absoluité) qui les permet mais bien par rapport à un agglomérat de systèmes (qu’on peut nommer super-système) internes à cette totalité des totalités, par lesquels se forme un système de valeurs
![]() il est désormais possible de décrire le mouvement des systèmes de connaissance du sujet se déployant dans l'Espace-temps (qui est en réalité la structure renfermant les trois propriétés de Multiplicité-Différence-Richesse permettant un tel mouvement) vers la Totalité.
il est désormais possible de décrire le mouvement des systèmes de connaissance du sujet se déployant dans l'Espace-temps (qui est en réalité la structure renfermant les trois propriétés de Multiplicité-Différence-Richesse permettant un tel mouvement) vers la Totalité.
Cela se produit dans un cycle métarécursif que j'ai nommé l'Onde (voir ma discussion avec Larkamboise) intriquant les notions d'Absolu et de Relatif.
Pour plus de précisions :
Voir uniquement le texte dans les spoils en "Partie 1" et "Partie 2" ![]()
- https://m.jeuxvideo.com/forums/message/1159367302
- https://m.jeuxvideo.com/forums/message/1159367726
Ce cycle considère, en ce qu'il a d'inhéremment contenu en lui, l'importance capitale de chaque sémantique qui permettrait de le parcourir sous une de ces modalités ; sans quoi il ne pourrait justement se présenter comme l'unité cyclique intriquant les dualités. Il porte en lui et intrique la positivité ainsi que la négativité des systèmes de connaissance qu'il synthétise.
Par delà l’apparente opposition de l’un et l’autre terme, au sein d'un tel mouvement, les antagonismes doivent toujours in fine être reconduits à l’unité sous-jacente par laquelle leur contradiction est subsumée.
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------
III ○ Ce mouvement se fait troisièmement sous un aspect transfigurant en ce qu'il comporte en lui un irréductible chaos, une irréductible entropie, une irréductible transformation, une irréductible relativité, une irréductible incomplétude, une irréductible émergence et en ce que cet aspect qu'il possède en lui est intriqué et même une condition sina que non de son harmonie, de ses sémantiques, de son ascension, de sa continualisation, de sa pertinence, de sa réalité... Ce mouvement ne peut se montrer comme une vérité absolue et immuable telle qu'on pourrait la nier de toute relativité externe, de tout chaos, de toute incomplétude ; puisque c'est tout simplement là nier une condition nécessaire qui fait sa substance, l'idée qu'il est justement un mouvement perpétuel, un parcours, une émergence continue et non une stagnation. D'où l'exemple de l'attracteur étrange de Lorenz : à l'instar de ce dernier, nous n'aurions pu aboutir à l'harmonie finale de la structure, à sa continuité, (Le mouvement/l'Onde/L'hélicoïde d'un côté et les ailes de papillon formées par l'attracteur de Lorenz de l'autre) sans l'irréductible part de chaos, d'incomplétude et d'entropie y ayant mené.
Je suis totalement incapable de ta rigueur, je me suis pas suffisamment entrainé à ça. Mais rien n'empêche de prendre du plaisir pour autant, ça ruine juste définitivement toute prétention.
Je donne certes une forme d'importance à la rigueur argumentative mais je pense que n'importe qui peut me dépasser en faisant les efforts pour, qui ne sont pas colossaux.
---------------------------------------------------------------------------------------------------------------------------------------------------------
Depuis quelques mois je reprend cette question qui me cuit le cul et dont tu dis qu'elle permet de formaliser une arithmétique : c'est quoi un entier ?
Je pense que ta question est pertinente et cache en fait en elle une rupture entre deux domaines :
I ○ Un domaine logique, formel et mathématique où l'on traite de systèmes, de leur syntaxe et leur sémantique, de langage, de théories avec des axiomes/postulats dont on découle la véracité et/ou la fausseté de certaines propositions descriptibles dans le langage du système selon certaines relations/règles imputées au système.
II ○ Un domaine phénoménologique, épistémologique (au sens de lié à une théorie de la connaissance) et de sciences cognitives où l'on traite de phénomènes, de notions, de concepts, d'intuitions, de catégories et de mécanismes cognitifs.
---------------------------------------------------------------------------------------------------------------------------------------------------------
On peut répondre à ta question en passant par ces deux domaines, mais les deux réponses (une pour chaque domaine) seront en réalité très significativement différentes, quoique liées sous une modalité quelconque.
La réponse à ta question qui passe par le domaine I n'expose pas une généalogie du concept d'entier, car ce n'est pas ce qui l'intéresse. Ce à quoi elle aspire, c'est de partir de données intuitives primitives comme la simple idée de "compter" afin d'organiser le tout dans un formalisme et une systématicité extrêmement rigoureux et précis, à des fins pragmatiques en science et en technologie.
Ainsi donc lorsqu'on formalise et définit les entiers en logique mathématique (sous le sens donc entendu dans mon post sur les deux théorèmes d'incomplétude de Gödel), on se contente de les construire sous la forme d'un ensemble (l'ensemble des entiers naturels puis l'ensemble des entiers relatifs) grâce à des postulats et règles qui sont tirées de l'intuition la plus fondamentale. On ne se peine cependant pas à établir une généalogie du concept d'entier, à expliquer comment nous aurions pu en aboutir cognitivement/épistémiquement aux idées du "0", du "1", du "+", de "compter" et de "collection" qui font la substance conceptuelle d'un entier. C'est en réalité en passant dans le domaine II que nous répondons à de telles problématiques.
---------------------------------------------------------------------------------------------------------------------------------------------------------
On tentera donc de répondre à ta question en passant par les deux domaines.
Réponse par le domaine I:
Nous cherchons à construire l'ensemble des entiers (pour l'instant naturels) qu'on notera ℕ afin de répondre à la question "Qu'est-ce qu'un entier ?", car une fois ayant construit cet ensemble, il nous suffit de dire qu'un entier est un élément de ce dernier.
---------------------------------------------------------------------------------------------------------------------------------------------------------
1 - L'entier chez Euclide dans les Éléments
Dans le livre VII, Euclide donne aux entiers la simple définition : « L'unité est ce relativement à quoi tout objet est appelé Un. » Cette abstraction lui permet de définir ensuite le nombre (entier naturel) comme « collection d'unités ».
On peut voir qu'il en reste à l'intuition et à l'abstraction les plus fondamentales et ne se peine pas à formaliser rigoureusement l'ensemble des entiers ℕ, car il n'avait pas d'intérêt pragmatique à aller plus loin.
---------------------------------------------------------------------------------------------------------------------------------------------------------
2 - Construction par les cardinaux chez Frege
Frege a songé (dans Les Fondements de l'arithmétique, 1884) à définir les entiers en termes de classe de bijectabilité.
Cette idée consiste à définir chaque entier n comme le rassemblement de tous les ensembles ayant n éléments.
Cette définition se heurte au paradoxe de Russell si l'on souhaite qu'un tel rassemblement soit, aussi, un ensemble.
Ceci car, sauf pour l'entier 0, identifié à l'ensemble contenant uniquement l'ensemble vide, pour tout autre entier n le rassemblement des ensembles ayant n éléments est une classe propre et donc n'est pas un ensemble.
En mathématiques, la notion de classe généralise celle d'ensemble. Les deux termes sont parfois employés comme synonymes, mais la théorie des ensembles distingue ces deux notions. Un ensemble peut être vu comme une collection d'objets, mais aussi comme un objet mathématique, qui en particulier peut lui-même appartenir à un autre ensemble. Ce n'est pas forcément le cas d'une classe, qui est une collection d'objets que l'on peut définir, dont on peut donc parler, mais qui ne forme pas nécessairement un ensemble. Quand une classe n'est pas un ensemble, elle est appelée classe propre. Elle ne peut alors pas être élément d'une classe (ni, a fortiori, d'un ensemble).
Les paradoxes de la théorie des ensembles, comme le paradoxe de Russell, montrent la nécessité d'une telle distinction. Ainsi la propriété « ne pas appartenir à soi-même » (x ∉ x) définit une classe mais pas un ensemble. L'existence d'un tel ensemble mènerait à une contradiction.
La définition de Frege conduit donc à une impasse. Pour en sortir, les mathématiciens ont cherché à définir un représentant dans chaque classe de bijectabilité, appelé cardinal de chacun des éléments de la classe. Cela peut être réalisé par un axiome garantissant la possibilité du choix d’un tel représentant dans chaque classe de bijectabilité. Un cardinal a est dit fini s’il est différent de a + 1. Les entiers naturels sont définis comme les cardinaux finis.
- 0 = Card(∅)
- 1 = Card ({a})
- 2 = Card ({a, b})
---------------------------------------------------------------------------------------------------------------------------------------------------------
3 - Construction de ℕ par la théorie des ensembles
Quelle que soit la manière d’introduire les entiers naturels, l’existence d’un ensemble les contenant tous, repose sur une forme ou une autre de l’axiome de l’infini.
Dans le domaine de la théorie des ensembles, l'axiome de l'infini est l'un des axiomes de la théorie des ensembles de Zermelo-Fraenkel, qui assure l'existence d'un ensemble infini, plus précisément d'un ensemble qui contient une représentation des entiers naturels.
Si les entiers naturels sont introduits avant la théorie des ensembles, celle-ci étant construite comme une extension de l’arithmétique, l’axiome de l’infini sous sa forme la plus simple s'énonce : il existe au moins un ensemble (infini) contenant tous les entiers naturels.
Si les entiers naturels sont introduits comme les cardinaux finis, l’existence peut être démontrée à partir de l’axiome : il existe au moins un ensemble infini. On montre que tout cardinal fini est inférieur au cardinal d’un ensemble infini. Par ailleurs, on montre que pour tout cardinal, il existe un ensemble des cardinaux qui lui sont inférieurs. L’ensemble des cardinaux inférieurs au cardinal d’un ensemble infini contient donc tous les entiers naturels.
Un ensemble dénombrable est un ensemble qui a le même cardinal que l'ensemble des entiers naturels (on précise parfois « infini dénombrable », dénombrable pouvant aussi signifier « fini ou de même cardinal que ℕ »). Le cardinal du dénombrable, celui de ℕ, est le plus petit cardinal infini, il est noté ℵ0 ,aleph-zéro.
L'ensemble des entiers naturels ℕ est muni des deux opérations d'addition "+" et de multiplication "*".
Elles sont :
- Des lois de compositions internes. Une loi de composition interne est une application qui, à deux éléments d'un ensemble E, associe un élément de E.
Ainsi : x ∈ ℕ, y ∈ ℕ : x + y ∈ ℕ | x*y ∈ ℕ
- Associatives : x ∈ ℕ, y ∈ ℕ, z ∈ ℕ : (x + y) + z = x + (y + z) | (x*y)*z = x*(y*z)
- Commutatives : x ∈ ℕ, y ∈ ℕ : x + y = y + x | x*y = y*x
- Munies d'un élément neutre (0 pour l'addition "+", 1 pour la multiplication "*") Un élément neutre (ou élément identité) d'un ensemble pour une loi de composition interne est un élément de cet ensemble qui laisse tous les autres éléments inchangés lorsqu'il est composé avec eux par cette loi. : x ∈ ℕ, 0 ∈ ℕ, 1 ∈ ℕ : x + 0 = x | x*1 = x
- Distributives entre elles : x ∈ ℕ, y ∈ ℕ, z ∈ ℕ : x*(y + z) = x*y + x*z
- Pour le cas de la multiplication seulement, elle est munie d'un élément absorbant, qui est 0 Un élément absorbant (ou élément permis) d'un ensemble pour une loi de composition interne est un élément de cet ensemble qui transforme tous les autres éléments en l'élément absorbant lorsqu'il est combiné avec eux par cette loi. Il est l'opposé conceptuel de l'élément neutre. : x ∈ ℕ, 0 ∈ ℕ : x*0 = 0
Elles font de l'ensemble des entiers naturels ℕ un semi-anneau.
ℕ est aussi muni d'une relation de divisibilité. La division euclidienne d'un entier (appelé dividende) par un autre (appelé diviseur et nécessairement non nul) est illustrée par le rangement d'une collection de n entiers représentant le dividende en un rectangle dont un côté représente le diviseur. Le nombre de rangées complètes représente alors le quotient tandis que l'éventuelle rangée incomplète représente le reste, nécessairement strictement inférieur au diviseur.
Il est aussi ordonné pour la relation d'ordre ("≤") usuelle induite par l'addition, qui lui donne une structure de bon ordre, c'est-à-dire que toute partie non vide admet un plus petit élément. Cette propriété est à la base du raisonnement par récurrence.
Les propriétés de la relation d'ordre en ℕ sont :
- x ∈ ℕ, y ∈ ℕ : (x ≤ y) ∨ (ou) (x ≥ y) (relation d'ordre total)
- x ∈ ℕ : (x ≤ x) (réflexivité)
- x ∈ ℕ, y ∈ ℕ : (x ≤ y) ∧ (et) (x ≥ y) ⇒ (x = y) (antisymétrie)
- x ∈ ℕ, y ∈ ℕ, z ∈ ℕ : (x ≤ y) ∧ (x ≤ z) ⇒ (x ≤ z) (transitivité)
- x ∈ ℕ, y ∈ ℕ, z ∈ ℕ : (x ≤ y) ⇒ (x + z) ≤ (y + z)
- x ∈ ℕ, y ∈ ℕ : (x ≥ 0) ∧ (y ≥ 0) ⇒ (x*y) ≥ 0
---------------------------------------------------------------------------------------------------------------------------------------------------------
4 - Construction de ℕ par l'axiomatique de Peano
Quelle que soit la façon d'introduire les entiers naturels, ceux-ci ont les mêmes propriétés fondamentales à partir desquelles on développe l'arithmétique. Richard Dedekind et Giuseppe Peano en ont proposé indépendamment des axiomatisations qui étaient essentiellement équivalentes. Il s'agissait d'axiomatisation que l'on dit parfois aujourd'hui du second ordre : la notion d'ensemble (ou de prédicat) est supposée connue et n'est pas prise en compte par l'axiomatisation. Voici une présentation moderne de ces axiomes (dits axiomes de Peano) :
- L'élément appelé zéro et noté 0, est un entier naturel ;
- Tout entier naturel n a un unique successeur, souvent noté s(n) ou S n (ou autres variantes) ;
- Aucun entier naturel n'a 0 pour successeur ;
- Deux entiers naturels ayant le même successeur sont égaux ;
- Si un ensemble d'entiers naturels contient 0 et contient le successeur de chacun de ses éléments, alors cet ensemble est égal à ℕ.
Le premier axiome permet de poser que l'ensemble des entiers naturels n'est pas vide, le second que le successeur est une fonction, le quatrième que cette fonction est injective, le troisième qu'il possède un premier élément (ces deux axiomes assurent que l'ensemble des entiers naturels est infini). Le cinquième est une formulation du principe de récurrence.
Une fonction f est dite injective ou est une injection si tout élément de son ensemble d'arrivée a au plus un antécédent par f, ce qui revient à dire que deux éléments distincts de son ensemble de départ ne peuvent pas avoir la même image par f.
Formellement :
Une fonction f : X → Y est injective si pour tout y ∈ Y, il existe au plus un x ∈ X tel que f(x) = y, ce qui équivaut à :
- ∀x ∈ X, ∀x' ∈ X : (f(x) = f(x') ⇒ x = x')
L'implication précédente équivaut à sa contraposée :
- ∀x ∈ X, ∀x' ∈ X : (x ≠ x' ⇒ f(x) ≠ f(x'))
Ainsi la fonction f(x) = x est injective sur ℝ car l'on ne peut trouver une image telle qu'elle a plus d'un antécédant, mais la fonction f(x) = x² sur ℝ ne l'est pas, puisque l'on peut bien trouver une image telle qu'elle a plus d'un antécédent. Par exemple, 4 a pour deux antécédents 2 et -2 puisque 2² = 4 et (-2)² = 4.
De façon encore plus formelle, dire du triplet (E, c, f) qu'il satisfait les axiomes de Peano, c'est dire qu'il satisfait les propriétés suivantes :
- E est un ensemble ayant c pour élément (c ∈ E) ;
- f est une fonction de E dans lui-même (loi de composition interne) ;
- c ∉ Im(f) ;
- f est injective ;
- Toute partie F de E contenant c et stable par f (c'est-à-dire telle que f(F) ⊂ F) est égale à E.
Im(f) correspond à l'ensemble image de la fonction f. On appelle image d'une fonction f (d'un ensemble A vers un ensemble B) (f : A → B) l'image directe par f de l'ensemble de départ A. C'est donc le sous-ensemble de B contenant les images de tous les éléments de A et uniquement ces images. On le note Im(f).
Plus formellement :
- Im(f) = {y ∈ B | ∃x ∈ A, f(x) = y} = {f(x) | x ∈ A} = f(A)
Ainsi la fonction f(x) = x sur ℝ a pour ensemble image ℝ lui-même (Im(f) = ℝ), tandis qu'une fonction telle que f(x) = 1 a pour ensemble image un simple singleton égal à {1} (Im(f) = {1}).
La formulation de la propriété 5 contient une quantification (universelle) sur les parties de E : une telle propriété est dite du second ordre. Une telle structure est un modèle des axiomes de Peano, vu comme axiomes en logique du second ordre.
En vertu du second théorème d'incomplétude de Gödel, la non-contradiction de ces axiomes entre eux n'est pas conséquence de ces seuls axiomes : on ne peut pas prouver la cohérence de l'arithmétique dans l'arithmétique.
---------------------------------------------------------------------------------------------------------------------------------------------------------
5 - Construction de l'ensemble des entiers relatifs (noté ℤ) à partir de ℕ
Afin d'aller de l'ensemble ℕ à l'ensemble ℤ, il suffit en fait globalement d'ajouter un axiome, celui de l'existence d'un élément symétrique pour l'addition "+" pour tout entier naturel.
Soit E un ensemble muni d'une loi de composition interne * admettant un élément neutre e ∈ E. Soient deux éléments a et b de E.
- Si a*b = e, a est dit élément symétrique à gauche de b et b est dit élément symétrique à droite de a
- Si a*b = b*a = e, a est dit élément symétrique de b
Un élément de E qui admet au moins un symétrique à droite est dit symétrisable à droite ; s'il admet au moins un symétrique à gauche, il est dit symétrisable à gauche ; s'il admet au moins un élément symétrique, il est dit symétrisable.
Tout entier relatif x de ℤ possède un élément symétrique pour l'addition, noté -x et nommé opposé.
Cela s'écrit :
- ∀x ∈ ℤ, ∃ y ∈ ℤ : x + y = 0 (0 étant l'élément neutre par rapport à l'addition dans ℤ)
L'ensemble ℤ des entiers relatifs peut donc être vu comme le symétrisé du semi-anneau ℕ des entiers naturels. Il est ce que l'on nomme un anneau.
Cet axiome (si on le saisit bien) et ce qui en découle suffit ainsi à définir les nombres négatifs et par extension l'étendue des opérations qu'il nous est permis d'user en ℤ. Par exemple, il nous permet en distinction avec ℕ d'exprimer la différence de deux entiers naturels quelconques. Entre autres significations de la différence, on peut citer la position sur un axe orienté par rapport à un point de référence (un axe à positions discrètes, c'est-à-dire discontinues) ; le déplacement depuis une position d'origine, dans un sens ou dans l'autre ; ou encore la variation d'une valeur entière, donc comptée en unités (variation positive pour un gain, négative pour une perte).
La principale raison de l'introduction des nombres négatifs est la possibilité de résoudre toutes les équations de la forme :
- a + x = b, où x est l'inconnue et a et b sont des paramètres.
Dans l'ensemble des entiers naturels, seules certaines de ces équations ont une solution.
- 5 + x = 8 si et seulement si x = 3
- 9 + x = 4 n'a pas de solution dans l'ensemble des entiers naturels. Elle possède une solution dans l'ensemble des entiers relatifs qui est -5.
---------------------------------------------------------------------------------------------------------------------------------------------------------
Fin de la réponse par le domaine I
Cette réponse fût longue, car l'on a essayé d'explorer le maximum de formalisations, de définitions et de systématisations des entiers au cours de l'histoire des mathématiques avec la rigueur et les précisions qu'elles ont impliqué. La réponse qui passe par le domaine II sera significativement plus courte, car je ne vais pas opérer par la même intransigeance qu'avec celle du domaine I, en rapport avec le formalisme des domaines mêmes qui en traitent.
---------------------------------------------------------------------------------------------------------------------------------------------------------
Réponse par le domaine II :
La notion d'entier naturel est bien probablement issue de la notion de collection : le nombre entier est avant tout conçu comme un cardinal. Certains objets ou animaux, tout en étant distincts les uns des autres, peuvent admettre une désignation commune, du fait de leur ressemblance ou d'une autre caractéristique partagée. Leur rassemblement constitue une collection, tel un troupeau de vaches, un collier de perles, un tas de pierres.
Le nombre est en germe dans l'énumération d'une collection, c'est-à-dire le fait de faire défiler tous ses éléments, un à un et sans répétition. Il prend consistance dans le constat que deux énumérations simultanées (d'un troupeau vers un enclos et de cailloux dans un sac, par exemple) se terminent soit toujours en même temps, soit toujours en décalage. Le nombre est enfin représenté lorsque le sac de cailloux ou le bâton à encoches est utilisé pour indiquer une quantité.
Cependant, le concept d'entier ne naît véritablement que lorsqu'il est départi de son représentant, c'est-à-dire lorsqu'il ne représente plus ni cailloux, ni encoches, ni vache : il y a là une première abstraction où chaque objet est considéré comme une unité pure et sans qualité. Ce processus mental est connu sous le nom d'abstraction : il est fait abstraction de la qualité de l'objet pour s'intéresser uniquement à la quantité. Une seconde abstraction mène alors à la considération de ces unités comme une collection d'unités.
Selon cet article de Science&Vie :
- Lien : https://www.science-et-vie.com/article-magazine/sciences-cognitives-on-sait-ou-se-situe-le-sens-des-nombres
« Une équipe de neuroscientifiques hollandais a localisé une aire cérébrale dans le cortex pariétal, derrière le haut des oreilles, dont les neurones ont la capacité de reconnaître les petites quantités d’objets. Chez des volontaires visionnant des images de pois, de triangles ou d’astérisques en nombre croissant, l’IRM fonctionnelle a révélé l’existence de groupes de neurones qui s’activent respectivement en réponse à un, deux, trois objets… et ainsi de suite jusqu’à sept. Plus étonnant, dans cette aire, les neurones sont organisés de manière ordonnée : ceux qui répondent au « trois » suivent ceux qui répondent au « deux », etc. Une telle organisation n’était jusqu’ici connue que dans les régions cérébrales impliquées dans les cinq sens. Pour le toucher, par exemple, il existe une carte cérébrale représentant toutes les zones corporelles stimulées tactilement. Selon les chercheurs, en plus de la quantité, d’autres concepts abstraits pourraient être représentés de manière similaire dans le cerveau. »
Le cortex pariétal est considéré comme un cortex associatif hétéromodal. C'est-à-dire qu'il joue un rôle important dans l'intégration des informations issues des différentes modalités sensorielles (vision, toucher, audition). Cette région du cerveau est impliquée dans la perception de l'espace et dans l'attention et, plus particulièrement, le cortex pariétal supérieur est impliqué dans le système visuel et dans le contrôle visuomoteur des mouvements, notamment des saccades oculaires.
Au cours de l'évolution de l'homme et des macaques et chimpanzés, le cortex pariétal, tout comme le lobe frontal, a subi une importante expansion corticale, c’est-à-dire que la taille de cette région a augmenté plus vite que les autres régions cérébrales.
Le cortex associatif désigne les régions du cerveau impliquées dans des opérations complexes de traitement de l'information. Contrairement à d'autres portions du cortex cérébral comme les aires dites « primaires » (sensorielles ou motrices), le rôle fonctionnel des régions associatives est plus difficile à identifier ; elles sont par exemple impliquées dans les processus cognitifs complexes liés à :
- l'intégration multisensorielle qui permet, par exemple, d'associer un signal visuel et un signal auditif ;
- la perception ;
- l'abstraction ;
- la mémoire ;
- le langage ;
- la planification ;
Contrairement à d'autres animaux, la majeure partie du cortex cérébral humain est constituée de cortex associatif, en particulier au niveau des lobes frontaux et pariétaux.
En effet, dans chaque hémisphère cérébral, 75 % du tissu cortical constitue le cortex associatif, le reste étant des régions spécialisées, comme les cortex sensoriels et moteurs. Le cortex associatif est aussi appelé « aires associatives », car il est composé de différentes aires, auxquelles on attribue des fonctions différentes. Elles se distinguent des autres aires car elles reçoivent des afférences de plus d'un système sensoriel, par exemple vision, audition etc... Elles participent donc à la genèse de notre perception du monde, qui intègre sans les décomposer les différentes modalités perceptives. Le cortex associatif permet la formation de nos perceptions qui sont une interprétation de nos sensations, une mise en relation de ces sensations avec notre expérience, nos intuitions et nos connaissances.
Plus d'informations :
- https://fr.wikipedia.org/wiki/Cortex_c%C3%A9r%C3%A9bral
- https://fr.wikipedia.org/wiki/Cortex_associatif
- https://fr.wikipedia.org/wiki/Lobe_pari%C3%A9tal#top-page
- https://fr.wikipedia.org/wiki/Lobe_frontal
- https://fr.wikipedia.org/wiki/Intuition
- https://fr.wikipedia.org/wiki/Entendement
- https://fr.wikipedia.org/wiki/Raison
![]()
